Linear Programming Word Problems
Purplemath
What are the constraints they "forget" to mention?
When you are doing a linear programming word problem, you are dealing with a (pretend) real-world situation. In this context, you will need to remember the understood (and thus usually omitted) constraints; namely, that you can't (generally) have negative amounts of inputs.
This omitted fact requires that you remember to add non-negativity constraints for each of your graphing variables; namely, x ≥ 0 and y ≥ 0.
- A calculator company produces a scientific calculator and a graphing calculator. Long-term projections indicate an expected demand of at least 100 scientific and 80 graphing calculators each day. Because of limitations on production capacity, no more than 200 scientific and 170 graphing calculators can be made daily. To satisfy a shipping contract, a total of at least 200 calculators much be shipped each day.
If each scientific calculator sold results in a $2 loss, but each graphing calculator produces a $5 profit, how many of each type should be made daily to maximize net profits?
The question asks for the optimal number of calculators, so my variables will stand for numbers of calculators:
x: number of scientific calculators produced
y: number of graphing calculators produced
Since they can't produce negative numbers of calculators, I have my first two constraints; namely, x ≥ 0 and y ≥ 0. However, as it turns out, I can ignore these constraints in this particular exercise, because they've already given me minimums:
x ≥ 100
y ≥ 80
The exercise also gives maximums:
x ≤ 200
y ≤ 170
The minimum shipping requirement gives me another constraint:
x + y ≥ 200
For graphing purposes, I'll restate this constraint as:
y ≥ −x + 200
The profit relation will be my optimization equation:
P = −2x + 5y
So my entire system is:
P = 2x + 5y, subject to:
100 ≤ x ≤ 200
80 ≤ y ≤ 170
y ≥ −x + 200
The feasibility region graphs as:
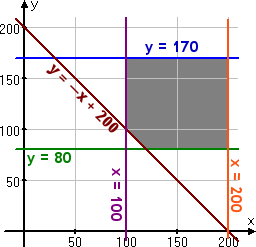
The corner points are at (100, 170), (200, 170), (200, 80), (120, 80), and (100, 100). When you test these points in the optimization equation, you should obtain the maximum value of profit P = 650 at (x, y) = (100, 170). Interpreting this within the context of the original word problem, the solution will be "100 scientific calculators and 170 graphing calculators".
(Yes, you can also find the answer just using logic: If the one kind loses you money and the other makes you money, obviously you'll want to maximize production of what makes you money.)
- You need to buy some filing cabinets. You know that Cabinet X costs $10 per unit, requires six square feet of floor space, and holds eight cubic feet of files. Cabinet Y costs $20 per unit, requires eight square feet of floor space, and holds twelve cubic feet of files. You have been given $140 for this purchase, though you don't have to spend that much. The office has room for no more than 72 square feet of cabinets. How many of which model should you buy, in order to maximize storage volume?
The question ask for the number of cabinets I need to buy, so my variables will stand for that:
x: number of model X cabinets purchased
y: number of model Y cabinets purchased
Naturally, x ≥ 0 and y ≥ 0. I have to consider the costs and the floor space (that is, the footprint of each unit), while maximizing the storage volume, so costs and floor space will be my constraints, while volume will be my optimization equation.
cost: 10x + 20y ≤ 140, or y ≤ −(½)x + 7
space: 6x + 8y ≤ 72, or y ≤ −(¾)x + 9
volume: V = 8x + 12y
This system (along with the first two constraints) graphs as:
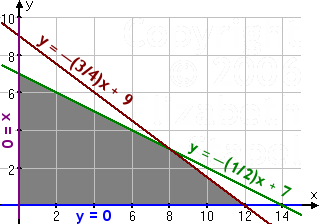
The corner points are at (0, 0), (8, 3), (0, 7), and (12, 0). When you plug them into the optimization equation, you should obtain a maximal volume of 100 cubic feet by buying eight of model X and three of model Y.
© 2024 Purplemath, Inc. All right reserved. Web Design by 