Linear Programming: An Example & A Word Problem
Purplemath
Linear programming is often viewed as being quite difficult but, especially in our two-variable context, it's not so much that the process is hard, so much as that the process requires you to bring so many topics together to solve any one given exercise.
You'll need to be good at graphing straight lines, understanding inequalities (in a graphing context), solving systems of linear equations (to find corner points), and evaluation (to find the maximum / minimum of the optimization equation). So make sure that you're solid on these topics before attempting these exercises.
What are the steps for linear programming?
To solve linear-programming exercises:
- Solve the inequalities for y, if possible.
- For each inequality, use the "equals" version to graph the lines. For instance, y − x + 4 ≤ 0 would convert to y = x − 4 for graphing.
- Graph each of the equation lines, and then shade according to the inequality symbols. The overlap is the feasibility region (that is, it's the area within which all valid solutions will lie).
- Pair up the equations for lines that cross each other in order to create systems of linear equations; solve these systems for the coordinates of the corners (that is, for the coordinates of the vertices) of the feasibility region.
- Test each corner's coordinates in the optimization equation they gave you.
- If you're needing to maximize, then take the corner that gives the largest answer to the optimization equation; otherwise, take the corner that gives the smallest answer.
- If the system of inequalities arose from a word problem, then go back and make sure that you are interpreting the values correctly according to the context.
Let's do another exercise that's just the inequalities and equations, before we try a word problem.
- Given the following constraints, maximize and minimize the value of z = −0.4x + 3.2y.
Okay; this system has a *lot* of inequalities. Four of the inequalities have one variable isolated on one side of the inequality symbol, which is the easier format for graphing. So now I'll solve the fourth and fifth constraints to isolate a variable:
The feasibility region looks like this:
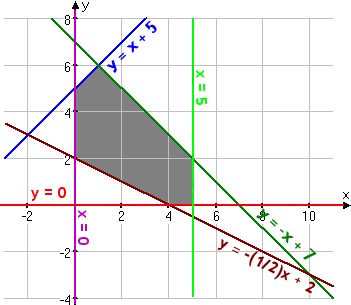
Take note of the purple line for x = 0 and the red line for y = 0. These are the y- and x-axes, respectively. When you deal (in later word problems) with situations based on real physical situations, you will almost always have the contraints that neither x nor y can be negative. So you should expect to see these constraints on a regular basis.
Also notice the vertical light green line for x = 5. Any time you have one variable that's set equal to just a number, then you'll have a vertical or horizontal line.
From the graph, I can see which lines cross to form what corners, so I know which lines to pair up in order to verify the vertex coordinates. I'll start at the top of the shaded area and work my way clockwise around the edges:
y = −x + 7
y = x + 5
−x + 7 = x + 5
2 = 2x
1 = x
y = (1) + 5 = 6
corner point at (1, 6)
y = −x + 7
x = 5
y = −(5) + 7 = 2
corner point at (5, 2)
x = 5
y = 0
[nothing to do]
corner point at (5, 0)
y = 0
y = (−½}x + 2
(0) = (−½)x + 2
(½)x = 2
x = 4
corner point at (4, 0)
y = (−½)x + 2
x = 0
y = (−½)(0) + 2
y = 0 + 2 = 2
corner point at (0, 2)
x = 0
y = x + 5
y = (0) + 5 = 5
corner point at (0, 5)
Now I'll plug each corner point into the optimization equation, z = −0.4x + 3.2y:
(1, 6): z = −0.4(1) + 3.2(6) = −0.4 + 19.2 = 18.8
(5, 2): z = −0.4(5) + 3.2(2) = −2.0 + 6.4 = 4.4
(5, 0): z = −0.4(5) + 3.2(0) = −2.0 + 0.0 = −2.0
(4, 0): z = −0.4(4) + 3.2(0) = −1.6 + 0.0 = −1.6
(0, 2): z = −0.4(0) + 3.2(2) = −0.0 + 6.4 = 6.4
(0, 5): z = −0.4(0) + 3.2(5) = −0.0 + 16.0 = 16.0
The max and min points are the points that give the largest and smallest values, respectively, when plugged into the optimization equation. Looking at my list, I see that my answer is:
maximum is 18.8 at (1, 6)
minimum is −2 at (5, 0)
When you are given the inequalities, linear-programming exercise are pretty straightforward, if perhaps sometimes a bit time-consuming. The hard part is usually the word problems, where you first have to figure out what the inequalities actually are. So I'll show how to set up some typical linear-programming word problems.
How do you solve linear programming word problems?
To solve a linear-programming word problem:
- Read through the entire exercise.
- Figure out what the exercise is asking for, using your translation skills.
- Pick variables to stand for the unknowns; label them clearly.
- Create inequalities for the various stated constraints. Don't forget to add the "understood" constraints when, in context, the variables cannot be negative.
- Create the optimization equation.
- Solve the linear programming system.
- Interpret the algebraic solution in terms of the original context.
Let's take a look at how this works in practice.
- At a certain refinery, the refining process requires the production of at least two gallons of gasoline for each gallon of fuel oil. To meet the anticipated demands of winter, at least three million gallons of fuel oil a day will need to be produced. The demand for gasoline, on the other hand, is not more than 6.4 million gallons a day.
If gasoline is selling for $1.90 per gallon and fuel oil sells for $1.50/gal, how much of each should be produced in order to maximize revenue?
The question asks for the number of gallons which should be produced, so I should let my variables stand for "gallons produced".
x: gallons of gasoline produced
y: gallons of fuel oil produced
(How did I know which variable to assign to the values? I didn't. There is no one right way. I could have used other variables, or reversed how x and y were matched up; it wouldn't have mattered. The numerical answer would still have been the same.)
Since this is a "real world" problem, I know that I can't have negative production levels, so the variables can't be negative. This gives me my first two constraints: namely:
x ≥ 0
y ≥ 0
Since I have to have at least two gallons of gas for every gallon of oil, then:
x ≥ 2y
If you're not sure about this inequality — and many people have emailed with questions about this, so you wouldn't be alone — then try plugging some numbers in. For instance, if they make three gallons of fuel oil, so y = 3, then they have to make at least twice as many gallons of gasoline. "Twice as many" as three is six. Then x ≥ 6, and 6 = 2y.
Keep plugging in numbers until the inequality makes sense to you.
For graphing, of course, I'll use the more manageable form "".
The winter fuel-oil demand condition says that y ≥ 3,000,000; note that this constraint eliminates the need for the "y ≥ 0" constraint. (Yes, one constraint can alter or eliminate another constraint. Real life is messy. Just go with it.) The gas demand condition says that x ≤ 6,400,000.
I need to maximize revenue R. The revenue from each of gas and fuel oil is the product of the per-gallon price and the number of gallons sold; the total revenue is the sum of the revenue from each. So the optimization equation is R = 1.9x + 1.5y. Then the model for this word problem is as follows:
R = 1.9x + 1.5y, subject to:
x ≥ 0
x ≤ 6,400,000
y ≥ 3,000,000
Using a scale that counts by millions (so "y = 3" on the graph means "y is three million"), the above system graphs as follows:
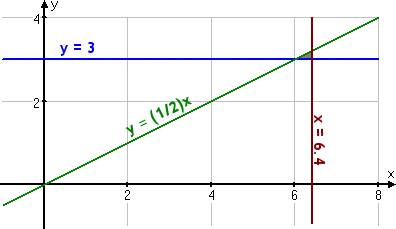
Taking a closer look, I can see the feasibility region a little better:
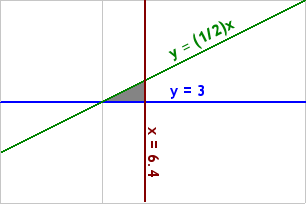
To complete the exercise, plug the coordinates of the corner points — at (6.4m, 3.2m), (6.4m, 3m), and (6m, 3m) — into the optimization equation.
You should get a maximal solution of R = $16.96m at (x, y) = (6.4m, 3.2m).
© 2024 Purplemath, Inc. All right reserved. Web Design by 