Systems of Linear Equations: Gaussian Elimination
Purplemath
Solving three-variable, three-equation linear systems is more difficult, at least initially, than solving the two-variable, two-equation systems, because the computations involved are more involved; there are just so many opportunities for careless mistakes to creep in. (I speak from painful experience.) So, when moving on from two-variable linear systems to more complicated situations, you will need to be very neat in your working, and you should plan to use lots of scratch paper. Lots and lots of scratch paper.
Content Continues Below
(The methodology for solving these larger systems of equations is an extension of the two-variable solving-by-addition method, so make sure you know this method well and can consistently use it correctly.)
Though the method of solution is based on addition/elimination, trying to do actual the actual addition tends quickly to become confusing, so there is a systematized method for solving three-or-more-variables linear systems. This method is called "Gaussian elimination".
(This solution method is named after Carl Friedrich Gauss, though Europeans had actually gotten this method from Isaac Newton a couple centuries earlier, who had come up with it independently about fifteen hundred years after the Chinese had developed it.)
Let's start simple, and work our way up to messier examples.
- Solve the following system of equations.
5x + 4 y – z = 0
10y – 3z = 11
z = 3
It's fairly easy to see how to get started in solving this system. The third equation in the system, the one at the bottom of the stack above, is a simple one-variable equality; namely, that z = 3. The second equation, the middle one in the stack above, has only the variables y and z. The simplest next step for me, then, it to substitute the z-value from the third equation back into the second equation. Then I'll solve the resulting one-variable equation for the value of y; in other words, I'll use that second equation to back-solve for y.
10y – 3(3) = 11
10y – 9 = 11
10y = 20
y = 2
This gives me the second value in this three-variable system. The only variable left is x. The first equation in the system, the one at the top of the stack above, contains this variable. I already have the values of y and z, so I'll plug their value in for their variables in the first equation, and back-solve for x.
5x + 4(2) – (3) = 0
5x + 8 – 3 = 0
5x + 5 = 0
5x = –5
x = –1
This is the third value for the solution to this system of equations. Keeping in mind that the variables will be listed in this three-coordinate point alphabetically, my answer is:
(x, y, z) = (−1, 2, 3)
Affiliate
The reason this system was easy to solve is that the system was "upper triangular"; this refers to the equations having the form of a triangle in the upper corner, because the first row contained terms with all three variables, the second row contained only terms with the second and third variable, and the third row contained a term only with the third variable. Outlining this region creates that upper-corner triangle, as shown below.
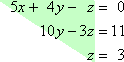
(This formation is also called "echelon" form (pronounced "ESH-eh-lahn") or "row-echelon" form, from the military definition of "echelon" being where each row (of soldiers or tanks or whatever) is shorter than the one immediately behind it. In this case, each row (of variable terms) in the matrix of equations is shorter than the row above it.)
The point is that, in this format, the system is simple to solve. And Gaussian elimination is the method we'll use to convert systems to this upper triangular form, using the "row operations" (that is, the multiplying through, the dividing through, and the adding down) that we saw when we learned the "addition/elimination method" of solving systems of equations on the previous page.
Content Continues Below
- Solve the following system of equations using Gaussian elimination.
–3x + 2y – 6z = 6
5x + 7y – 5z = 6
x + 4y – 2z = 8
No equation is solved for a variable, so I'll have to do the multiplication-and-addition thing to simplify this system. In order to keep track of my work, I'll write down each step as I go. But I'll do my computations on scratch paper. Here is how I did it:
The first thing to do is to get rid of the leading x-terms in two of the rows. For now, I'll just look at which rows will be easy to clear out; I can switch the rows' order later, if needed, to put the system into upper triangular form.
There is no rule that says I have to use the x-term from the first row, and, in this case, I think it will be simpler to use the x-term from the third row, since its coefficient is simply "1". So I'll multiply the third row by 3, and add it to the first row. I first do my actual computations on scratch paper:
![multiplying R3 by 3 gives [3x + 12y −6z = 24]; adding this version of R3 to the original R1 gives [-3x + 2y - 6z = 6] + [3x + 12y - 6z = 24] = [14y - 12z = 30]](systems/lin021.gif)
...and then I write down the results:
![system of equations showing updated R1: [[14y − 12z = 30][5x + 7y − 5z = 6][x + 4y − 2z = 8]]](systems/lin025.gif)
(When we were solving two-variable systems on the previous page, we could multiply a row, rewriting the system off to the side, and then add down. There is no space for this in a three-variable system, which is why we need the scratch paper.)
Please take careful note: I didn't actually do anything to the third row — I had used the third row, but I hadn't actually changed the third row — so I merely copied it over, unchanged, into the new matrix of equations. I neither changed nor used the second row, so I copied it over, unchanged, to the new matrix as well. The only row that was actually changed was the first row; in the new matrix, you can see that I wrote in the results of my scratch-work.
Do not confuse "using" with "changing".
(To make my steps clear for the grader (and for me, when I review later for the test), I have annotated the arrow between the two steps to show that I'd multiplied the third row by three, and then had added the result to the first row, in order to get a new first row.)
I generally prefer to work with smaller numbers, and I notice that all the coefficients in the (new) first row are even. So, to get smaller coefficients, I'll multiply the first row by one-half (or, which is the same thing, divide through by 2):
![after multiplying R1 by one-half, R1 is now [7y - 6z = 15]; the system is now [[7y − 6z = 15][5x + 7y − 5z = 6][x + 4y − 2z = 8]]](systems/lin026.gif)
Now that's I've removed the x-term from R1, I turn my attention to R2. I could divide this row by −5 and then add this to the third row (leaving the in-use second row unchanged), but this will give me loads of fractions in the third row. I'd like to avoid fractions as long as possible. So, instead, I'll multiply the third row by −5 and add the result to the second row (leaving the in-use third row unchanged). I do this work on scratch paper:
![[5x + 7y - 5z = 6] + [-5x - 20y + 10z = -40] = [-13y + 5z = -34]](systems/lin022.gif)
I haven't done anything with the first row, so I'll copy it to the new system unchanged. I worked with the third row (in my scratch-work), but I only worked on the second row, so the second row will be updated in the new system, but the third row will be copied over unchanged.
![after updating R2, the system now is [[7y - 6z = 15][−13y + 5z = −34][x + 4y − 2z = 8]]](systems/lin027.gif)
Advertisement
Okay, now thex-column is cleared out except for the leading term in the third row. So, to work further toward triangular form, I next have to work on the y-column.
Affiliate
Note: Since the third equation has an x-term, I cannot use it on either of the other two equations any more — or I'll undo my progress in clearing those rows of x-terms. I can work on the equation (using other rows to clear the y-term), but not with it (that is, I cannot apply it to the other two rows).
Looking at the first and second rows, I see that I could divide the first row by 7 and the second row by 13, and then the y-terms will cancel. But this will give me loads of fractions. I could multiply to the least common multiple, which is 91, but then the numbers will start getting kinda big. Neither of these options is "wrong"; it's just that I'm lazy, so I'm going to see if there might be a better option.
If I multiply the first row by 2 and add the result to the second row, this will give me a leading 1 in the second row. I won't have gotten rid of the leading y-term in the second row, but I will have converted it (without bogging down in fractions) to a form that is simpler to deal with. (You should keep an eye out for this sort of simplification.) First I do the scratch work:
![multiplying R1 by 2 gives [14y − 12z = 30]; adding this to R2 gives [-13y + 5z = -34] + [14y - 12z = 30] = [y - 7z = -4]](systems/lin023.gif)
I update the second row, leaving the first (that I'd worked with but not on) and third (with which I'd done nothing) unchanged.
![adding 2R1 to R2 results in the updated system [[7y - 6z = 15][y - 7z = -4][x + 4y − 2z = 8]]](systems/lin028.gif)
Now I can use the second row to clear out the y-term in the first row. I'll multiply the second row by −7 and add the result to the first row. First I do my scratch work:
![multiplying R2 by −7 gives [−7y + 49z = 28]; adding this to R1 gives [7y - 6z = 15] + [-7y + 49z = 28] = [43z = 43]](systems/lin024.gif)
I worked with R2, but only on R1; I did nothing with R3. So I leave R2 and R3 unchanged, updating the system with the new R1.
![updating R1 gives an updated system: [[43z = 43][y - 7z = -4][x + 4y − 2z = 8]]](systems/lin029.gif)
I can now see what the value of z is but, just to be thorough, I'll divide through on the first row by 43. Then I'll rearrange the rows to put them in upper-triangular form:
![dividing R1 by 43 gives [z = 1]; rearranging the rows gives: [[x + 4y − 2z = 8][y − 7z = −4][z = 1]]](systems/lin030.png)
Now I can start the process of back-solving:
y – 7(1) = –4
y – 7 = –4
y = 3
That's a second variable done. Now I'll do the final back-solving:
x + 4(3) – 2(1) = 8
x + 12 – 2 = 8
x + 10 = 8
x = –2
I now have values for each of the three variables. I found these values in, as it happened to turn out, reverse-alphabetical order. I'll need to remember to write my solution with the variables in the correct, alphabetical order.
(x, y, z) = (−2, 3, 1)
Note: There is nothing sacred about the steps I used in solving the above system; there was nothing special about how I solved this system. You could work in a different order or simplify or combine different rows in different ways, and still come up with the correct answer. These systems are sufficiently complicated that there is unlikely ever to be only one right way of computing the answer. So don't stress over "how did she know to do that next?", because there is no rule. I didn't "know"; I just did whatever I happened to notice first, or whatever happened to struck my fancy; I did whatever seemed simplest or whatever first sprang to mind.
Don't worry if you would have used completely different steps from a classmate or your instructor. As long as each step along your way is correct, then you will come up with the same answer.
In the above example, I could have gone further in my computations and been more thorough-going in my row operations, clearing out all the y-terms other than that in the second row and all the z-terms other than that in the first row. This would then have been the entire process, from beginning to end:

When a system is reduced in this way, I can just read off the values of x, y, and z directly from the system; I don't have to bother with the back-substitution. This more-complete method of solving is called "Gauss-Jordan elimination" (the "Jordan" part being named after Wilhelm Jordan). When the equations are reduced to this point, where you can simply read off the solution, the system is said to be in "reduced" row-echelon form.
Many textbooks only go as far as Gaussian elimination, but I've always found it easier to continue on and do Gauss-Jordan. And no instructor should ever count off for your doing extra steps or being "too complete" in your work. Unless otherwise specified, do what you like.
Note that I did two row operations at once in that last step before switching the rows. As long as I'm not working with and working on the same row in the same step, this is okay. In that last step, I was working with the first row, using it to work on the second and third rows.
And yes, solving systems of linear equations (by hand) is often, even usually, this long and involved. Like I said before: lots and lots of scratch paper.
The next page has more worked examples.
URL: https://www.purplemath.com/modules/systlin6.htm
You can use the Mathway widget below to practice solving systems of linear equations with three or more variables (or skip the widget and continue on to the next page). Try the entered exercise, or type in your own exercise. Click the button and select "Solve using Gaussian Elimination" to compare your answer to Mathway's.
Please accept "preferences" cookies in order to enable this widget.
(Click "Tap to view steps" to be taken directly to the Mathway site for a paid upgrade.)
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()




