Using the Quadratic Formula to Solve Systems of Non-Linear Equations
Intro ConceptsGraphing ConceptsSolving Simple SystemsSolving Intermediate SystemsSolving Advanced Systems
Purplemath
How can the Quadratic Formula help solve a system of nonlinear equations?
When a nonlinear equation has a term where the x and y are multiplied together, applying the Quadratic Formula can allow you to solve for one of the variables in terms of the other.
Content Continues Below
In other words, sometimes you'll need to use old tools in new ways when solving the more advanced systems of non-linear equations. The example below demonstrates how the Quadratic Formula is sometimes useful in solving systems; it also shows how involved your computations might get. (Hint: Very.)
- Solve the following system of equations:
x2 − xy + y2 = 21
x2 + 2xy − 8y2 = 0
This system represents an ellipse and a set of straight lines. (Yes, really; the second equation actually graphs as two straight lines.) If I solve each equation above for y=, then I can enter the "plus-minus" equations into my graphing calculator to check my work.
Plugging the first quadratic above in the Quadratic Formula, and solving for y in terms of x, I get:
Affiliate
In order to apply the Quadratic Formula to the first equation, I had to regard everything that wasn't a y (or y2) as a coefficient on that term. This meant that some values for b and c in the Formula contained variables. This is completely okay; this is a perfectly legitimate way of applying the Formula.
Now I'll solve the second quadratic with the Formula, too:
Affiliate
(Where did those absolute-value bars come from? Recall that, technically, the square root of x2 is the absolute value of x. That's how I did that simplification in the next-to-last line above. And this absolute value will matter shortly.)
The absolute value of x in the second equation above gives two cases for the values of y:
If x < 0, then | x | = −x, so:
If x > 0, then | x | = x, so:
In either case, I get the same two solution expressions for the corresponding values of y:
Since I derived these "y=" solution-equations from the second of the original equations, I will plug them into the first equation to solve for some actual numerical values:
If , then I get:
I got these two numerical values by assuming that . Plugging these x-values into that equation, I get:
If, on the other hand, , then I get:
I got these two numerical values by assuming that . Plugging these x-values into that equation, I get:
Then my four solutions to this system are these points:
Warning: Do not try to write the solution points as "" or "", because this is not true. Not all combinations of these x-values and y-values are solution points. Don't be sloppy; write the solution out correctly.
By the way, my graph of the system looks like this:
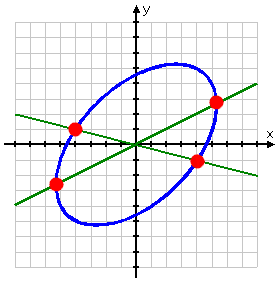
(To graph the ellipse using the traditional methods, you would have to do a "rotation of axes", a process you probably won't see until calculus, if at all.)
Content Continues Below
By the way, there is another method of doing the algebra for the above exercise, because the quadratic in the second equation happens to be factorable. (This factorability is NOT generally true, but you should try to remember to check, just in case.) If you factor the second equation and solve for x in terms of y, you get:
x2 + 2xy − 8y2 = 0
(x + 4y)(x − 2y) = 0
x + 4y = 0 or x − 2y = 0
x = −4y or x = 2y
Advertisement
You can plug these expressions for x= into the first equation in place of x, and solve the resulting equation for the corresponding y-values.
This last example (the first way I worked it) is about as complicated as these things ever get. But if you plug away and work neatly and completely, you should be able to arrive at the solution successfully. And if you have a graphing calculator (and the time), try doing a quick graph to verify your answers visually.
You'll hardly ever need to plug an equation into the Quadratic Formula in order to create expressions containing just one of the variables. But when nothing works, see if the Quadratic Formula might help.
URL: https://www.purplemath.com/modules/syseqgen6.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()




