Inverting Functions with Restricted Domains
Defs / Inverting a GraphIs the Inverse a Function?Finding InversesWorked ExamplesQuarter-CirclesProving Inverses
Purplemath
The graph of a parabola will not pass the Horizontal Line Test; there are loads of horizontal lines that will cross the graph twice. So the inverse of a parabola's quadratic function will not itself be a function.
However, sometimes a non-invertible function can be converted into an invertible one by restricting the domain.
Content Continues Below
In the case of the parabola, if we use only one "side" (or one "half") of the parabola, then the graph will pass the Horizontal Line Test.
How do you find the inverse of a function with a restricted domain?
Affiliate
Advertisement
The steps for finding the inverse of a function with a restricted domain are exactly the same as the steps for finding the inverse of any other function:
- Replace "f(x)" with y.
- Try to solve the equation for x=.
- Swap the x's and the y.
- Replace y with "f−1(x)"
Then restrict the inverse function, as needed, so that the range and domain of the inverse match the domain and range, respectively, of the original function.
- Find the inverse function of y = x2 + 1, x ≤ 0.
On the previous page, we saw that this function, absent the domain restriction, is not invertible. The only difference with this function is that the domain has been restricted to include only the negative half of the x-axis; that is, the function has been restricted to just the left-hand half of the parabola. This restriction makes the graph look like this:
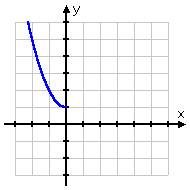
This function passes the Horizontal Line Test, so it will have an inverse that is also a function.
(fyi: Just about any time they give you a problem where they've taken the trouble to restrict the domain, they've also almost always given you something whose inverse will also be a function. However, you should take care with the algebra and draw a nice picture, because it may require some extra effort to show that the inverse is a function. And, if nothing else, the restricted domain on the function will require a restricted range on the inverse function.)
In this case, since the domain is x ≤ 0 and the range (from the graph) is y ≥ 1, then the inverse will have a domain of x ≥ 1 and a range of y ≤ 0.
I start by solving for "x =":
y = x2 + 1
y − 1 = x2
I'd figured out the domain and range of the inverse function before I went and found that function. By figuring out the domain and range of the inverse in advance, I know that I have to choose the negative sign for the square root on my inverse function to be the correct inverse of the original function:
Now I'll switch the x and y; the new "y =" is the inverse:
(The "x ≥ 1" restriction is confirmed by the fact that the expression x − 1 is inside a square root. The only way for the square root to be defined is for x − 1 ≥ 0.)
So my answer is:
inverse:
this inverse is also a function
The above example illustrates the answer to this question:
Why is the domain restricted on some functions?
When you're trying to find inverses of functions, sometimes the domains of those functions must be restricted in order to make the function invertible. In order to make sure that the original function passes the Horizontal Line Test, part of the function may need to be eliminated.
Content Continues Below
- Find the inverse of . Determine whether the inverse is also a function, and find the domain and range of the inverse.
For this function, the domain restriction comes from the fact that x is inside a square root. Usually I wouldn't bother writing down "x ≥ 2", because I know that x-values less than 2 would give me negative numbers inside the square root. But the restriction is useful in this case because, together with the graph, it will help me determine the domain and range on the inverse:

The domain (given in the exercise statement) is x ≥ 2; the range (found from the graph) is y ≤ 0. Then the domain of the inverse will be x ≤ 0; the range will be y ≥ 2.
Affiliate
Now I need to find my inverse:
y2 = x − 2
y2 + 2 = x
x2 + 2 = y
f−1(x) = x2 + 2
This inverse function graphs as a parabola, where I'd started with half of a (sideways) parabola. Since I already figured out the domain and range — in particular, the domain of the inverse is x ≤ 0 — I know that I need to take the negative half of the parabola. So my answer is:
inverse: f−1(x) = x2 + 2
the inverse is a function
domain x ≤ 0
range y ≥ 2
- Find the inverse of f (x) = x2 − 3x + 2, x ≤ 1.5
With the domain restriction, the graph looks like this:
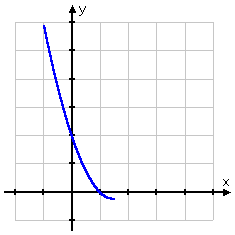
From what I know about graphing quadratics, the vertex is at (x, y) = (1.5, −0.25), so this graph is the left-hand half of the parabola. And this half of the parabola passes the Horizontal Line Test, so the (restricted) function is invertible. But how to solve for the inverse? I start as usual:
f(x) = x2 − 3x + 2
y = x2 − 3x + 2
Now I solve for "x=" by using the Quadratic Formula:
0 = x2 − 3x + 2 − y
0 = x2 − 3x + (2 − y)
Since x ≤ 1.5, then I want the *negative* square root:
Then, after renaming, the inverse is given by:
Yeah, sometimes inverses can be messy.
URL: https://www.purplemath.com/modules/invrsfcn4.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()