Finding the Inverse of a Function
Defs / Inverting a GraphIs the Inverse a Function?Restricted DomainsWorked ExamplesQuarter-CirclesProving Inverses
Purplemath
How do you find the inverse of a function?
The steps for finding the inverse of a function, where they've given you a formula for the function, are these:
- Replace "f(x)" with y.
- Try to solve the equation for x=.
- Swap the x's and the y.
- Replace y with "f−1(x)"
Content Continues Below
Advertisement
Note: Some textbooks and instructors have you swap the variables (Step 3 above) before solving (Step 2 above). If you're supposed to find inverses that way, then the steps are:
- Replace "f(x)" with y.
- Swap the x's and the y.
- Try to solve the equation for y=.
- Replace y with "f−1(x)"
I will be using the order in the first set of steps above. Whichever method you're supposed to use, make sure that you practice it enough that you remember the steps on the next test.
- Find the inverse of y = 3x − 2.
Here's how the inverse-finding process works: I start with my original function:
y = 3x − 2
Now I'll try to solve for "x =":
Once I have "x=", I'll switch x and y; the new "y=" is the inverse.
Then the inverse is:
Affiliate
If you need to find the domain and range of the inverse, look at the original function and its graph. The domain of the original function is the set of all allowable x-values; in this case, the function was a simple polynomial, so the domain was "all real numbers".
The range of the original function is all the y-values you'll pass on the vertical axis; in this case, the graph of the function is a straight line that goes on for ever in either direction, so the range is also "all real numbers".
To find the domain and range of the inverse, just swap the domain and range from the original function.
- Find the inverse of , state the domain and range, and determine whether the inverse is also a function.
Since the variable is in the denominator, this is a rational function. Also, because I can't have division by zero, the domain of this function is x ≠ 5. A fraction is zero when its numerator is zero, which this numerator never will be, so the range at least contains the restriction that y ≠ 0. From what I know about rational functions and vertical asymptotes (of which, this function has one), I know that the graph will go forever upward and forever downward, so the range is indeed everything other than y = 0. I'll use this to find the domain and range of my inverse.
Here's the algebra for finding that inverse, starting with the original function:
I multiply the denominator up to the left-hand side of the equation:
y(x − 5) = −2
I take the y through the parentheses:
xy − 5y = −2
I get the x-stuff by itself on one side of the "equals" sign:
xy = 5y − 2
Then I solve for x=:
And then switch the x's and y's:
So I've found the inverse, and it's another rational function; in particular, the inverse is indeed a function.
The domain and range of this inverse function are the reverses of the original function's domain and range. So my answer is:
inverse:
domain: x ≠ 0
range: y ≠ 5
the inverse is a function
Content Continues Below
You may find yourself working with a function named f(x) instead of y. In that case, start the inversion process by renaming f(x) as y. Then follow the usual procedure. Once you find the inverse, rename the resulting y as f−1(x). (Why the swap? It's usually easier, in my experience, to work with y.)
Warning: The inverse-function notation is misleading; the "minus one" power in the inverse-function notation means "the inverse of the original function", not "the reciprocal of the expression". Don't confuse the two.
- Find the inverse of f (x) = x2 + 1, and state whether the inverse is a function.
There will be times when they give you functions that don't have inverses, and, from the graph of the given function, it's easy to see that this function can't possibly have an inverse, since it violates the Horizontal Line Test:
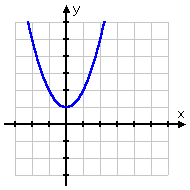
It is usually considered acceptable to draw the above graph, draw a horizontal line across it that crosses the graph twice, and then say something like "The inverse of this function is not itself a function, because of the Horizontal Line Test". But some teachers want to see the algebra anyway. Be sure to check with your teacher and verify what will be an acceptable answer -- and do this before the test!
What will this look like when I try to find the inverse algebraically? The Vertical Line Test says that I can't have two y's that share an x-value. That is, each x has to have a UNIQUE corresponding y value. But look at what happens when I try to solve for "x=":
Affiliate
My original function:
f (x) = x2 + 1
First, I'll swap out the f (x) for the simpler y:
y = x2 + 1
Now I try to solve for "x=":
y − 1 = x2
Well, I found the inverse, but is it a function? No; because, for any input x in the inverse, but I won't get a UNIQUE output y. Instead, I've shown that any given x-value will actually correspond to two different y-values, one from the "plus" on the square root and the other from the "minus". Because of this, my answer is:
inverse:
The inverse is not a function.
Any time you come up with a "±" sign, you can be pretty sure that whatever you've got is not a function.
URL: https://www.purplemath.com/modules/invrsfcn3.htm
You can use the Mathway widget below to practice finding the the inverse of functions. Try the entered exercise, or type in your own exercise. Then click the button and select "Find the Inverse" to compare your answer to Mathway's. (Or skip the widget and continue with the lesson.)
Please accept "preferences" cookies in order to enable this widget.
(Click "Tap to view steps" to be taken directly to the Mathway site for a paid upgrade.)
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()