Functions versus Relations
Purplemath
There are different ways of looking at functions. We will consider a few. But first, we need to discuss some terminology.
What is a relation in algebra?
A "relation" is just a relationship between two sets of information. Think of all the people in one of your classes, and think of their heights. The pairing of names and heights is a relation.
Content Continues Below
In relations and functions, the pairs of names and heights are "ordered", which means one comes first and the other comes second. To put it another way, we could set up this pairing so that either you give me a name, and then I give you that person's height; or else you give me a height, and I give you the names of all the people who are that tall. This pairing of information in an ordered fashion (always, say, the names first, with the heights second) creates what are called ordered pairs.
What are the domain and range of a relation?
Affiliate
The set of all the starting values in a relation is called the domain and the set of all the ending values is called the range. The domain is what you start with; the range is what you end up with; the domain is the x's, the range is the y's. (I'll explain more on the subject of domains and ranges later.)
In these ordered pairs, the pieces of information (names and heights, in our example) are called coordinates. If we're being technical, the first coordinate in any ordered pair is called the abscissa (abb-SISS-uh); the second coordinate is called the ordinate (ORR-dih-nitt). The set of all abscissas is the domain of the relation; the set of all ordinates is the range of the relation.
What is a function (in math)?
A function is a well-behaved relation, by which we mean that, given a starting point (that is, given an abscissa), we know the exactly one ending spot (that is, exactly one ordinate) to go to; given an x-value, we get only and exactly one corresponding y-value.
Note what this means: While all functions are relations (since functions do pair information), not all relations are functions. Well-behaved family members are a subset of all your relations; so also functions (being well-behaved) are a subset of all math relations. For a function, there will never be any choice of y-values; given an x-value, there will be precisely one y-value that can be paired with it.
What is an example of a function (in math)?
One example of a function would be a pairing of families with their current (primary) home addresses. Given a family, there will be only one address at which the family members live for most or all of the year. The set of all the addresses is the function's domain; the set of all the families is the range.
Another example of a function would be radius values and the areas of circles. Given a radius value r, the formula A = πr2 will spit out exactly one value for the area.
What is a real-world example of a relation that is not a function?
Advertisement
Let's return to our relation of your classmates and their heights, and let's suppose that the domain is the set of everybody's heights. Let's suppose that there's a pizza-delivery guy waiting in the hallway. (This is a college classroom and, yes, the pizza dudes/dudettes do deliver.) All the delivery guy knows is that the pizza is for the student in your classroom who is five-foot-five.
Now let the guy in. Who does he go to? What if nobody is five-foot-five? What if there are six people in the room that are five-five? Do they all have to pay? What if you are five-foot-five? And what if you're out of cash? And allergic to anchovies? Are you still on the hook? Ack! What a mess!
The relation with ordered pairs (height, name) is not well-behaved. Therefore, it is not a function. Given the relationship (x, y) = (five-foot-five person, name), there might be six different possibilities for y = name(for that height). For a relation to be a function, there must be only and exactly one y that corresponds to a given x.
What are some pictures of functions and relations?
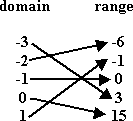
The above shows a function. You can tell that this is a function by tracing from each x to each y. There is only one y for each x; there is only one arrow coming from each x.

Ha! Bet I fooled some of you on this one! This is a function! There is only one arrow coming from each x; there is only one y for each x. It just so happens that it's always the same y for each x, but it is only that one y. So this is a function; it's just an extremely boring function!
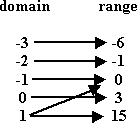
This one is not a function: there are two arrows coming from the number 1; the number 1 is associated with two different range elements. So this is a relation, but it is not a function.

Okay, this one's a trick question. Each element of the range that has a paired value from the domain. But what about that 16 in the domain? It is in the domain, but it has no range element that corresponds to it; there is no ordered pair with 16 as its abscissa. This won't work! So then this is not a function. Heck, it isn't even a relation!
How do you know if an equation is a function?
There are various ways to determine if an equation represents a function:
- You can solve the equation for "y=".
- The equation be entered into your graphing calculator's graph utility.
- The equation has only and exactly one y-value for each x-value.
The last option above has been turned into a test of equation graphs, called the Vertical Line Test.
Content Continues Below
What is the Vertical Line Test?
The Vertical Line Test (vlt) provides a graphical way of testing whether a relation is a function. If there is no place on the graph of a relation where a vertical line (that is, an up-and-down down) would cross twice, then the relation passes the test, and is a function. Now, what does all that mean?
Looking at this function stuff graphically, what if we had the relation that consists of a set containing just two points: {(2, 3), (2, −2)}? We already know that this is not a function, since x = 2 goes to each of y = 3 and y = −2.
If we graph this relation, it looks like:

Notice that you can draw a vertical line through the two points, like this:

This characteristic of non-functions was noticed by I-don't-know-who, and was codified in "The Vertical Line Test": Given the graph of a relation, if you can draw a vertical line that crosses the graph in more than one place, then the relation is not a function.
What is an example of applying the Vertical Line Test?
Consider the graph below:
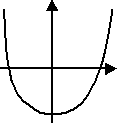
This graph shows a function, because there is no vertical line that will cross this graph twice.
Now consider the ellipse graphed below:

This graph does not show a function, because any number of vertical lines will intersect this oval twice. For instance, the y-axis intersects (crosses) the line twice.
What's a quick way to determine if it's a function or not?
Affiliate
One of the quickest ways to determine if a given formula or equation represents a function is to look at your graphing calculator. If the formula can be entered into the calculator (so the calculator can graph it or evaluate it or whatever), then it's a function; otherwise, not. What does this mean?
Thinking of all the graphing you've done, the simplest method for a given equation is to solve for "y=", make a T-chart, pick some values for x, solve for the corresponding values of y, plot your points, and connect the dots, yadda, yadda, yadda.
Not only is this useful for graphing, but this methodology gives yet another way of identifying functions: If you can solve for "y=", then it's a function. In other words, if you can enter it into your graphing calculator, then it's a function. The calculator can only handle functions. For example, 2y + 3x = 6 is a function, because you can solve for y:
2y + 3x = 6
2y = −3x + 6
On the other hand, y2 + 3x = 6 is not a function, because you can not solve for a unique y:
I mean, yes, this is solved for "y =", but it's not unique. Do you take the positive square root, or the negative? Besides, where's the "±" key on your graphing calculator? So, in this case, the relation is not a function.
By the way, you can also check this relation by using our first definition from above. Think of plugging in x = −1. Then we get y2 − 3 = 6, so y2 = 9, and then y can be either −3 or +3. That is, if we did an arrow chart, there would be two arrows coming from x = −1. This again shows that the relation is not a function.
URL: https://www.purplemath.com/modules/fcns.htm
You can use the Mathway widget below to practice determining if a relation is a function. Try the entered exercise, or type in your own exercise. Then click the button and select "Determine if the Relation is a Function" to compare your answer to Mathway's. (Or skip the widget, and continue with the lesson.)
Please accept "preferences" cookies in order to enable this widget.
(Click "Tap to view steps" to be taken directly to the Mathway site for a paid upgrade.)
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()