Circles: Definitions & Drawing
Purplemath
What is a circle?
A circle is a geometrical shape. It is defined as having a center, and being the set of all points that are a certain fixed distance from that center. (The fixed distance is called the radius of the circle.) The circle is not of much use in algebra since the equation of a circle isn't a function.
Content Continues Below
But you may need to work with circle equations in your algebra classes, probably in a chapter titled "Conics" (because reasons).
What was the original definition of a circle?
In primative terms (that is, in physical and non-algebraic terms), a circle was a geometric shape formed in sand with two sticks and some string.
- Drive one of the sticks firmly into the sand. This will be the circle's center.
- Tie the ends of the string together, forming a loop.
- Put this loop around the center stick and the other stick.
- Hold the other stick vertical at the furthest extent of the loop.
- With the end of this second stick in the sand, pull the stick around the center stick.
Once you've pulled the second stick all the way around once, the trace of the second stick is the circle.
What is the algebraic definition of a circle?
In algebraic terms, a circle is the figure formed by the set (or "locus") of points (x, y) at some fixed distance r from some fixed point (h, k). The value of r is called the "radius" of the circle, and the point (h, k) is called the "center" of the circle.
What is the circle equation?
The general equation of a circle is:
x2 + y2 + Dx + Ey + F = 0
The "center-radius" form of the equation is:
(x − h)2 + (y − k)2 = r2
...where the h and the k come from the center point (h, k) and the r2 comes from the radius value r.
If the center is at the origin, so (h, k) = (0, 0), then the equation simplifies to x2 + y2 = r2.
Affiliate
Note: The general form may be given in your book using different letters for the coefficients, but the center-radius form will use the same letters as shown above. The center is always denoted by (h, k) and the radius is always denoted by r.
What is the standard form of the circle equation?
Your textbook might refer to something called the "standard" form of the circle equaion. Unfortunately, "standard form" has no standard meaning that I've been able to determine, so you'll have to keep track of what your particular textbook intends by that term.
How can you switch between the center-radius form and the general form of the circle equation?
You can convert the center-radius form of the circle equation into the general form by multiplying things out and simplifying; you can convert in the other direction by completing the square.
The center-radius form of the circle equation comes directly from the Distance Formula and the definition of a circle. If the center of a circle is the point (h, k) and the radius is length r, then every point (x, y) on the circle is distance r from the point (h, k). Plugging this information into the Distance Formula (using r for the distance between the points and the center), we get:
You should practice until you can readily recognize this formula, because you will be expected to be able to read information from it.
Content Continues Below
How do you draw a circle in algebra?
To draw (that is, to graph) a circle in algebra (as opposed to drawing one in geometry, where you can use a compass), follow these steps:
- Draw a neat set of axes, and draw neat and consistent scales on those axes, by using a ruler.
- Plot the center point for the circle.
- Lightly sketch in marks, in each of the four directions (up, down, left, and right), from the center point.
- Lightly sketch in arcs between these four marks; it helps to rotate your paper for this step.
- Edit as needed, to obtain a circle that looks fairly smooth and round.
- Draw the circle with a heavier pencil, or with an ink-pen.
- Gently erase the marks you made in steps 3 through 5.
Here's an example of what that looks like:
- State the center and radius of the circle with the equation (x − 2)2 + y2 = 52, and sketch the circle.
The y2 term in the equation means the same thing as (y − 0)2, so the equation is really the following:
(x − 2)2 + (y − 0)2 = 52
Since the circle's equation is now in center-radius form, I can read the values directly: The center must be at (h, k) = (2, 0), and the radius must be r = 5.
To sketch, I'll first draw the dot for the center:

I can't draw a perfect circle, so I'll work in steps. First, in pencil, I'll rough in markers that are five units away from the center in each of the four easy directions (that is, directly up, down, left, and right from the center):
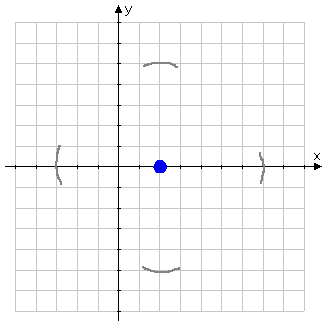
Then I'll rough in the curvy bits in between these markers, turning the paper as I go:
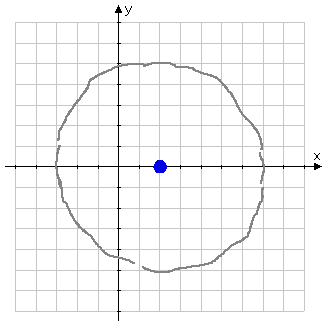
I'll make whatever corrections look useful, trying to make my circle look properly circular, and ink my final answer as a solid dark line:
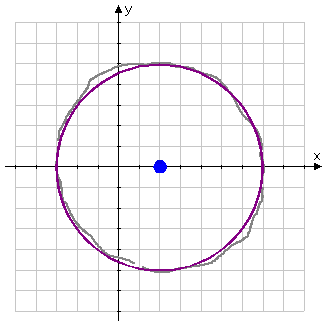
So that I'm handing in a nice-looking drawing, I'll erase the pencil marks from my roughing-in, and I'll copy my center and radius values that I found earlier.
center: (h, k) = (2, 0)
radius: r = 5
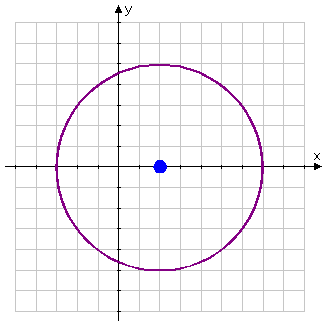
Hint: It can be very helpful to rotate your paper when you do your drawing, so as to end up with a circle that looks fairly round.
You can use the Mathway widget below to practice finding the center and radius of a circle (or skip the widget and continue on to the next page). Try the entered exercise, or type in your own exercise. Then click the button to compare your answer to Mathway's.
Please accept "preferences" cookies in order to enable this widget.
(Click "Tap to view steps" to be taken directly to the Mathway site for a paid upgrade.)
URL: https://www.purplemath.com/modules/circle.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()