Circles: More Examples
Purplemath
Circles and their equations can arise in many different contexts. Exercises based on these contexts will assume that you remember stuff from other classes.
For instance, you'll be expected to remember what a circle's tangent is.
What does it mean for a line to be tangent to a circle?
A line that is tangent to a circle is a line that touches the circle at only one point and which is, at that point, perpendicular to the radius line from the center to that same point.
This tangent-line fact, among others, is something they'll expect you to have learned in, and remembered from, a geometry class (possibly some years ago). And working with lines that are perpendicular brings in the topic of the slope of a straight line, which you'll be expected to remember from an algebra class. Et cetera.
Yeah. 🙄
- Find an equation for the circle centered at (1, −5) and tangent to the line 3x + 4y = 8.
For one line (or curve) to be tangent to another means that the lines just touch; they don't cross. In the context of circles, the tangent is perpendicular to the radius line from the center to that point on the circle. This tells me that I need to find the line perpendicular to 3x + 4y = 8 and passing through the point (1, −5), because the radius will lie on that line.
Also, the intersection point of the radius line and the given line will be a point on the circle. I can use this information to find the length of the radius.
First, I find the slope of the given line:
3x + 4y = 8
4y = −3x + 8
From the slope-intercept form of the line, I can see that the slope of the given line is −3/4, so my radius line to the intersection point, being perpendicular to the tangent line, must have a slope of m = 4/3. Plugging this and the center point into the point-slope equation of a straight line, I get:
This is the equation of the line that *contains* my radius line. (Remember that this line actually continues forever in either direction; the radius is only a short segment of that line.)
So now I have two lines; one is tangent to the circle, one contains a radius line of the circle, and their intersection point must then be a point on the circle itself. To find this intersection point, I'll take the two line equations and solve the system of equations that they create.
Since each of the two equations is already solved for "y=", I'll set the two opposite sides equal to each other, and solve for the remaining variable x. I'll start by multiplying through by 12 to clear all of the denominators.
−9x + 24 = 16x − 76
24+76 = 16x + 9x
100 = 25x
4 = x
I can plug this value into either of the original two equations to get the other coordinate of the point. Doing so tells me that y = −1, and thus that the point (4, −1) is a point on the circle. From this and the center point (which they gave me in the beginning), I can use the Distance Formula to find the length of the radius:
![d = sqrt[(1−4)^2 + (−5−(−1))^2] = sqrt[(−3)^2 + (−4)^2] = sqrt[9 + 16] = sqrt[25] = 5 = r](conics/circle08.gif)
So r = 5, and my equation is:
(x − 1)2 + (y + 5)2 = 25
What is the interior / exterior of a circle?
The interior of a circle is the set of all the points inside the circle's line, having a distance from the center of less than the length of the radius. The exterior of a circle is the set of all points outside the circle's line, having distances from the center greater than the length of the radius.
- Is the point (−2, 0) in the interior or exterior of the circle with equation (x − 3)2 + (y + 5)2 = 49?
Reading from the circle equation they gave me, I can see that the center of the circle is at (h, k) = (3, −5) and the radius is r = 7. To determine on which side (inside or outside) of the circle the point they asked about lies, I need to find the point's distance from the center, and compare that distance with the length of the radius.
First, I note that, because r = 7, then r2 = 49. Then, I take the coordinates of the circle's center and the point they gave me, and plug them into the Distance Formula, knowing that I'll be comparing the Formula's result with √49 = 7:
![d = sqrt[(3−(−2))^2 + (−5−0)^2] = sqrt[(5)^2 + (−5)^2] = sqrt[25 + 25] = sqrt[50] > sqrt[49] = 7 = r](conics/circle09.gif)
Since this distance is more than that of the radius, then:
This point is in the exterior.
At the beginning of this lesson, I'd mentioned that circles are not functions, which is part of why they can feel kind of tacked on to algebra, rather than being a proper part of algebra. You will be asked to graph circles, and you might like to check your work before you hand it in. But how, when your graphing calculator can only graphing functions?
How can my calculator graph a circle's equation?
To check your graphs, or to graph an equation to verify that it fits the requirements of an exercise, you can solve the circle equation for the two half-circle equations. Each of these half-circle equations will be a function, which you can plug into your graphing calculator.
For instance, (x − 3)2 + (y + 2)2 = 25 solves as follows:
![(y + 2)^2 = 25 − (x − 3)^2, y + 2 = ± sqrt[25 − (x − 2)^2], y = −2 ± sqrt[25 − (x − 3)^2]](conics/circle15.gif)
Your calculator can only graph y=, not y±. But you can split the "plus-minus" into two separate equations, each of which on its own is a function. The "plus the square root of" part is the top half of the circle; the "minus the square root of" part is the bottom half. Plug these two halves into your calculator as follows:
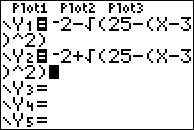
...and graph:
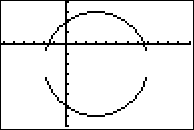
The standard calculator set-up, with the tickmarks on the x-axis being wider apart than on the y-axis, will make the graph look squashed; the above was done using the "Zoom-Square" setting. Even squashed, though, your graph should suffice to confirm that the circle is centered at or near (3, −2), with a radius at or near 5.
(The gap between the upper and lower halves of the circle is an artifact of the calculator's limitations. It can't understand graphing the bits that are close to vertical.)
Make sure you memorize the center-radius form of the equation, and practice how to complete the square, how to do quick but nicely round circle graphs, and how to use your graphing calculator to check your answers. Other than involving some messy computations, circles aren't too bad — as conics go.
© 2024 Purplemath, Inc. All right reserved. Web Design by 