Basic Trigonometric Ratios: Definitions
Purplemath
Right triangles are nice and neat, well-behaved, with their side lengths obeying the Pythagorean Theorem; namely, for any right triangle, the lengths of its sides a, b and c, where c is the longest of the three sides, it is always true that a2 + b2 = c2.
For any two right triangles where the measures (that is, the sizes) of the other two (that is, the non-right) angles the same are said to be "similar", in the technical sense that their corresponding sides are in proportion.
Content Continues Below
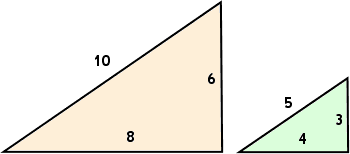
For instance, the following two triangles (not drawn to scale) have all the same angles, so they are similar, and thus corresponding pairs of their side-lengths are in proportion:
Affiliate
What does it mean to say "corresponding pairs are in proportion"?
When we say that "corresponding pairs of their side-lengths are in proportion", we mean that we can create fractions by taking the length of a side of one of the similar triangles (let's say the larger one, in this case), and divide it by the length of the corresponding side of the other similar triangle (here being the smaller one). When we do this division, we will find that each of these fractions reduces to the same value for a given pair of similar triangles.
For the above pair of similar triangles, making a fraction first from the hypotenue pair of side lengths (with the larger triangle's hypotenuse length being divided by the smaller triangle's hypotenuse length), the base pair of side lengths, and the height-line pair, we always get the same value of 2, as shown below:
ratios of corresponding sides:
(A different pair of similar triangles would likely have some other common ratio value. The value isn't as important as the fact that the fractions will all be equal, which is a property of similar triangles.)
We can also form ratios by dividing one side of one of the similar triangles by one of the other two sides of that same triangle. When we use the same sides in the same order to form the corresponding ratio for the other of the similar triangles, the two fractions will reduce to the same value. For our two triangles above (and again using the larger triangle's values as our numerators, and dividing by the smaller triangle's values), we get:
ratio of hypotenuse to base:
ratio of hypotenuse to height:
ratio of height to base:
Of course, we could have done the division in the other order; this gives us the reciprocals of the previous ratios, but the point is that the matching divisions still have matching ratio values:
ratio of base to hypotenuse:
ratio of height to hypotenuse:
ratio of base to height:
The resulting fractions are the reciprocals of the previous values, but the point here is that the two triangles' ratios still match. This also shows that there are actually six side-pair ratios that we can form for any two given similar triangles, and their values will be consistent.
Not only do the six ratios match for these two similar triangles, the ratios will in fact match for any and all right triangles similar to these two. To illustrate this, I nested the two triangles above, overlapping them at the base angle; then I extended (off toward the right) the lines for the base and hypotenuse. Then I dropped some vertical (dark green) lines from the hypotenuse line down to the base line, arriving at the picture below:
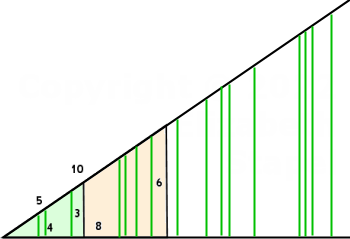
The vertical lines are height (or altitude) lines for just a few of the infinitely-many similar right triangles that can be formed from that one base angle. There is literally no end to the similar triangles that share this same base angle. And every single one of them will have the exact same ratio values.
Content Continues Below
When were trig ratios invented?
At some point around the fourth or fifth century AD, somebody very clever living in or around India noticed this consistency in the proportionalities of similar right triangles (that is, the consistency of the values of the six different ratios of right triangles sharing the same size of base angle), and started working on tables of ratios corresponding to those base angles. There would be one set of ratios for the one-degree angle in all 1-89-90 triangles, another set of ratios for the two-degree angle in all 2-88-90 triangles, and so forth. These ratios are called the "trigonometric" ratios for a right triangle.
Advertisement
These tables of ratio values are very long, in part because they include values for many of the angles with measures between whole-number degrees, too; and take some time to use. Depending on how accurate the instructor (or workplace application) needed your answer to be, you might be looking through more than twenty pages of trig tables (such as in this book), and still need to use interpolation or various formulas to get the numbers you actually needed.
Why were trig tables invented?
People needed trig tables because the computations required to derive these values (by hand) are long and complex. (Quora discussion) Working from pre-printed tables, probably in the back of a textbook or in a pocket reference manual, was the only practical way to do trig before electronic calculators became widely available. (Some people still use pocket references on the job, "in real life", even now, as demonstrated here.)
Affiliate
The college professor I had for my trigonometry class even mentioned once that trig exams in the past had been required to be very short, in order to allow for all the time that students would have to be spending with the rote process of table-value lookup. So be very glad that you've always got a calculator in your pocket in the form of a smartphone. Open the calculator app, turn your phone sideways, and just look at all the fancy stuff you can do! But trig exams, as Professor Gorowara noted with a twinkle in his eye, can nowadays be much longer, so... mixed bag, I guess?
Given a right triangle with a base angle designated as θ ("THAY-tuh"), we can label the hypotenuse (always the side opposite the right angle) and then label the other two sides "with respect to θ" (that is, in relation to the base angle θ that we're working with) including for values between whole-number degrees, too.
The side opposite the angle θ is the "opposite" side; and the other side, being the base of the triangle shown below, is the "adjacent" side.

For the same triangle, let's now look at the other non-right angle; namely, the angle at the triangle's upper right corner. We'll name it β ("BAY-tuh"). With respect to the angle β, the sides would be labelled differently. The base would now be the "opposite" side, and the height line would be the "adjacent" side, as shown below:

As you can see, the labels "opposite" and "adjacent" are relative to the angle in question. If you switch to the other angle (that is, if you switch to the other angle that *isn't* the right angle), the legs' labels will be switched, too.
Let's return to the first labelling we looked at, the one using the angle θ at the bottom left:

Rather than throw everything at you all at once, let's go step by step.
There are three sides to this right triangle; namely, the hypotenuse, the height line (which is the side opposite the angle), and the base at the bottom (which is the side adjacent to the angle). There are six ways to form ratios of the three sides of this triangle. In the following tables, I'll shorten the names from "hypotenuse", "adjacent", and "opposite" to "hyp", "adj", and "opp", respectively. The tables below show the six ratios in the center columns.
name | ratio | notation |
|---|---|---|
|
opp/hyp |
|
|
adj/hyp |
|
|
opp/adj |
|
name | ratio | notation |
|---|---|---|
|
hyp/opp |
|
|
hyp/adj |
|
|
adj/opp |
|
Ratios in same-color rows of each table are reciprocals of each other. For instance, the ratio in the pink row in the first table is "adj/hyp", while the ratio in the pink row in the second table is its reciprocal fraction "hyp/adj".
Each of these ratios has a formal name. These names have been been added to the left-hand columns of the tables below:
name | ratio | notation |
|---|---|---|
sine |
opp/hyp |
|
cosine |
adj/hyp |
|
tangent |
opp/adj |
|
name | ratio | notation |
|---|---|---|
cosecant |
hyp/opp |
|
secant |
hyp/adj |
|
cotangent |
adj/opp |
|
Each of these ratios' names has an abbreviated notation, which includes specification of the angle you're working with by using function notation, as shown in the right-hand columns of the completed tables below:
name | ratio | notation |
|---|---|---|
sine |
opp/hyp |
sin(θ) |
cosine |
adj/hyp |
cos(θ) |
tangent |
opp/adj |
tan(θ) |
name | ratio | notation |
|---|---|---|
cosecant |
hyp/opp |
csc(θ) |
secant |
hyp/adj |
sec(θ) |
cotangent |
adj/opp |
cot(θ) |
The ratios sine, cosine, and tangent are the "regular" trig ratios; the cosecant, secant, and cotangent are their respective reciprocal ratios (that is, the values of the flipped-over fractions for the "regular" ratios).
By the way, there is no requirement that Greek letters be used as the argument of (that is, the input to) a trig function. For instance, it's perfectly okay to use x, if you like.
What does SOH-CAH-TOA stand for?
Many students use the mnemonic "SOH-CAH-TOA" (pronounced "SOH-kuh-TOH-uh") to remember how to form the ratios for the sine, cosine, and tangent of a right triangle. The letters in this mnemonic stand for:
- Sine is Opposite over Hypotenuse
- Cosine is Adjacent over Hypotenuse
- Tangent is Opposite over Adjacent
How do the co-sine, -secant, and -tangent relate?
When two ratios have the same name other than the "co-" at the start of one of them, the pair are called "co-functions". Pairs of co-functions are related in how their graphs are shaped; each co-function's graph is the same shape as the original function, other than for being translated or transformed (that is, other than being moved sideways or flipped about a bit).
Specifically, the cosine looks just like the sine, but shifted a bit to the left; the cosecant is a left-shift of the secant; the cotangent is the tangent after flipping it upside-down and then shifting the result a bit to the left.
How did the trig ratios get their names?
The trigonometric ratios didn't get their current European names until the 12th century or so. The ratios' current names come to us as a result of those Middle-Ages Europeans making some mistakes when they translated Arabic texts. The history of trigonometry is rather tangled. [source]
URL: https://www.purplemath.com/modules/basirati.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()