Basic Trigonometric Ratios: Solving Triangles
Purplemath
When you're just getting started with trigonometric ratios, you'll likely begin by finding the trigonometric values (that is, the ratios) for a given triangle.
To find your answers, you'll just plug the lengths they've given you into the relevant trig ratio.
- List the values of sin(α), cos(α), sin(β), and tan(β) for the triangle below, accurate to three decimal places:
For either of the two non-right angles of this triangle, the hypotenuse has length 9.7. Right triangles have only one hypotenuse, so this value does not change with respect to the non-right angles.
For the angle α, the "opposite" side has length 6.5 and the "adjacent" side has length 7.2.
The sine ratio is "opposite over hypotenuse"; for this triangle, this means 6.5 over 9.7. I'll plug the given values into the definition of the sine:
The cosine of α is "adjacent over hypotenuse"; for this triangle, this means 7.2 over 9.7. I'll plug the given values into the definitions of cosine:
I keep in mind that "opposite" and "adjacent" are found with respect to the named angle. So, for the angle β, the opposite side has length 7.2 and the adjacent side has length 6.5.
Therefore, for the angle β, the sine is given by:
The tangent ratio is "opposite over adjacent". With respect to the angle β, the tangent's value is given by:
Rounding to three decimal places, I get:
sin(α) = 0.670
cos(α) = 0.742
sin(β) = 0.742
tan(β) = 1.108
Once you've memorized the trig ratios, you can start using them to find other values. To do this, you'll likely need to use a calculator. If your calculator does not have keys or menu options with "SIN", "COS", and "TAN", then now is the time to upgrade. Make sure you know how to use the calculator, too; the owners manual should have clear instructions.
(Yes, I know you've got a full-featured calculator on your phone. You also have texting and messaging apps, which could be used for, shall we say, "unsanctioned assistance" on tests. So you'll probably need a stand-alone calculator, too. Don't assume that your instructor will be chill with your using your mobile during an exam.)
With the six trig ratios for any right triangle, you can now begin to "solve" right triangles.
What does it mean to "solve" a right triangle?
"Solving a right triangle" refers to the process of taking partial information (such as the lengths of one of the triangle's sides, and the measure of one of the non-right angles), plugging this information into one or another of the six trigonometric ratios to create equations, and then solving these equations (often with the help of a calculator) to find the values of the missing side lengths or angle measures.
- In the triangle shown below, find the value of x, accurate to three decimal places.
They've given me an angle measure and the length of the side opposite this angle, and have asked me for the length of the hypotenuse. The sine ratio is "opposite over hypotenuse", so I can turn what they've given me into an equation:
I have to plug this into my calculator to get the value of x; the screen says that x = 190.047286.... Rounded this value to three decimal places, my answer is:
x = 190.047
Note: If your calculator displayed a value of 71.19813587... instead of 190.047286..., then check the "mode"; your calculator is set to "radians" rather than to "degrees". (You'll learn about radians later.)
- For the triangle shown below, find the value of y, accurate to four decimal places.
They've given me an angle, a value for the length of the adjacent side, and a variable for the length of the opposite side. The tangent ratio involves the lengths of the sides opposite and adjacent to an angle. With this ratio, I can form an equation that will let me solve for the value of the variable:
Plugging this into my calculator, I get y = 14.44183406..... Rounding to four decimal places, my answer is:
y = 14.4418
- Find the values indicated by the letters in the diagram below. Give each answer correct to the nearest whole number.
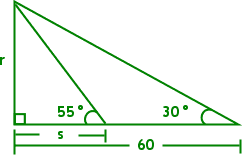
At first, this looks fairly intimidating. But then I notice that, to find the length of the height r, I can use the base angle 30° from the larger triangle and that triangle's full base length of 60, because is "opposite over adjacent", which is the tangent ratio.
I'll use this information to create my equation, which I'll then solve.
I'm supposed to the nearest whole number, so r = 35.
Now that I have the value of r, I can use r and the other base angle, 55°, to find the length of the other base, s, by using :
The instructions tell me to round to the nearest whole number, so my answer is:
r = 35, s = 25
If you use the pre-rounded value of 60 tan(30°), then your value for will be slightly different; it'll be more like 24.2559006.... This is why I discourage such severe rounding as "to the nearest whole number"; it can throw your values off by a lot.
Keep this in mind when you're doing your own work, especially for word problems. To get a usefully accurate answer, keeping as many decimal places as reasonably feasible can make a big difference by the end of the exercise.
Note: Since the sine and cosine ratios involve dividing a leg (one of the shorter two sides) by the hypotenuse (which is always the longest side), the ratio values will never be more than 1, because (some number) / (a bigger number) is always going to be smaller than 1. But you can have right triangles that are really wide and short or really tall and skinny, so "opposite" and "adjacent" can have *very* different values. This tells you that the tangent ratio, being (opposite) / (adjacent), can have very large and very small values, depending on the triangle.
So if you get a value for sine or cosine that is larger than 1, you should go check your work. On the other hand, if you get a huge value for tangent for some wonky triangle, you shouldn't be surprised.
© 2024 Purplemath, Inc. All right reserved. Web Design by 