Systems of Linear Inequalities: Special Cases
Purplemath
The solution region for the previous example was a bounded solution, because there were lines closing it in on all sides. That solution region was a triangle.
But, since the boundaries of the solution regions are formed by lines, and since lines won't necessarily intersect each other helpfully, there are other options, there are special cases, for solution regions. One special case is the system in which you obtain a solution which is "unbounded"; that is, the solution goes off forever in some direction or other.
What is an example of an unbounded solution?
- Solve the following system:
2x − y > −3
4x + y < 5
As usual, I first want to solve these inequalities for "y". I get the following rearranged system:
y < 2x + 3
y < −4x + 5
Each of these is a strict inequality, so I'll need to remember to draw my boundary lines as dashed lines. The lines themselves (representing the "or equal to" case, which doesn't apply here) are not going to be part of any solution to this system.
Graphing the first inequality, I get:
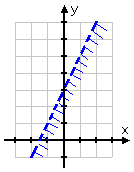
Drawing the second inequality, I get:
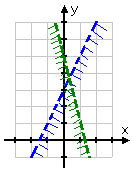
The solution is the lower region, where the two individual solutions overlap. The graph showing this overlap (along with the clearly dashed boundary lines) is my answer:
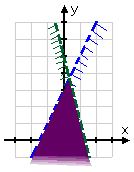
The kind of solution displayed in the above example is called "unbounded", because it continues forever in at least one direction (in this case, forever downward).
Note how I drew the lower end of the solution region. I didn't draw a sharp line across the bottom of my drawing; doing so would have implied the existence of some third line that formed a bottom to the region. But there is no bottom. So I let my shading get lighter as I approached the bottom of my graphing area.
If you have a solution region that's unbounded, make sure you draw it so it doesn't look bounded. Make your meaning clear.
Of course, there's always the possibility of getting no solution at all.
What is an example of a system with no solution?
- Solve the following system:
x − y ≤ −2
x − y ≥ 2
First I solve for y, and get the equivalent system:
y ≥ x + 2
y ≤ x − 2
I note that each of these is an "or equal to" inequality so the solution region, if any, will include the lines. So I'll be drawing my boundaries as solid lines.
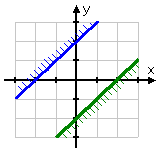
I graph the first inequality:
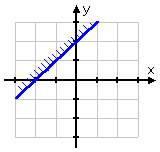
...and then the second:
But there is no place where the individual solutions overlap. (Note that the lines y = x + 2 and y = x − 2 never intersect, being parallel lines with different y-intercepts.)
Since there is no intersection of the two inequalities' individual solution regions, then there can be no solution to the system of inequalities. And therefore my answer to the exercise is:
no solution
When your answer is that there is no solution, you will probably be expected to say so, in writing, as I did above. In this one particular case, just the graph will probably not be sufficient; for full credit, state clearly what you mean.
© 2024 Purplemath, Inc. All right reserved. Web Design by 