Synthetic Division & Factoring
Purplemath
On the previous page, we saw how synthetic division can make it easier (and faster) find the zeroes of a polynomial.
Also, we noted that, given the zeroes (also called solutions, roots, and x-intercepts) of a polynomial, we can work backwards to find the factors of the polynomial.
How can synthetic division help with factoring?
Synthetic division is used for checking possible zeroes of a polynomial (these possible zeroes having been generated by the Rational Roots Test). If synthetic division confirms that x = b is a zero of the polynomial, then we know that x − b is a factor of that polynomial.
- Use synthetic division to determine whether x − 4 is a factor of −2x5 + 6x4 + 10x3 − 6x2 − 9x + 4
For x − 4 to be a factor of the given polynomial, then I must have x = 4 as a zero. (Remember that this is how we solved quadratics by factoring: We'd find the two factors, set each of the factors equal to zero, and solve. Here, we're working backwards from zeroes to factors.)
Using this information, I'll do the synthetic division with x = 4 as the test zero on the left:
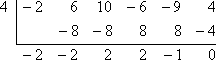
Since the remainder is zero, then x = 4 is indeed a zero of −2x5 + 6x4 + 10x3 − 6x2 − 9x + 4, so:
Yes, x − 4 is a factor of −2x5 + 6x4 + 10x3 − 6x2 − 9x + 4
- Find all the factors of 15x4 + x3 − 52x2 + 20x + 16 by using synthetic division.
Remember that, if x = b is a zero, then x − b is a factor. I'll start by using the Rational Roots Test (and maybe a quick graph on my calculator) to find a good value to test as possibly being a zero (that is, possibly an x-intercept on the graph). I'll try x = 1:
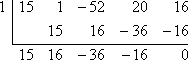
This division gives a zero remainder, so x = 1 must be a zero, which means that x − 1 is a factor. Since I divided a linear factor (namely, x − 1) out of the original polynomial, then my result has to be a cubic:
15x3 + 16x2 − 36x − 16
So I need to find another zero before I can apply the Quadratic Formula. I'll try x = −2:
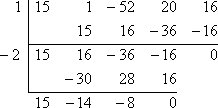
Since I got a zero remainder, then x = −2 is a zero, so x + 2 is a factor. Plus, I'm now down to a quadratic, 15x2 − 14x − 8, which happens to factor as:
(3x − 4)(5x + 2)
Then the fully-factored form of the original polynomial (namely, 15x4 + x3 − 52x2 + 20x + 16) is:
(x − 1)(x + 2)(3x − 4)(5x + 2)
- Given that
is a zero of x4 + 6x3 − 7x2 − 30x + 10, fully solve the equation x4 + 6x3 − 7x2 − 30x + 10 = 0.
Since they have given me one of the zeroes, I'll use synthetic division to divide it out:
![top row is −3+sqrt[11] | 1 6 −7 −30 10; middle row is |__−3+sqrt[11]__2__15−5sqrt[11]__−10_; bottom row is 1 3+sqrt[11] −5 −15−5sqrt[11] 0](polysolv/synth62.gif)
(You will probably want to use scratch paper for the computations required when manipulating the radical root.)
I only get these square-root answers from using the Quadratic Formula. Since the square-root part of the Formula is preceded by a "plus-minus" sign, then these square-root answers always come in pairs. Thus, if 
is a root, then so also 
must be a root.
So my next step is to divide by :
![top row is −3−sqrt[11] | 1 3+sqrt[11] −5 −15−5sqrt[11]; middle row is |__−3−sqrt[11]__0__15+5sqrt[11]_; bottom row is 1 0 −5 0](polysolv/synth63.gif)
I had started with a fourth-power polynomial. After the first division, I was left with a cubic (with very nasty coefficients!). After the second division, I'm now down to a quadratic (x2 + 0x − 5, or just x2 − 5), which I know how to solve:
Then the full solution is:
If you have studied complex numbers, then you may have exercises similar to the following:
- Given that 2 − i is a zero of x5 − 6x4 + 11x3 − x2 − 14x + 5, fully solve the equation x5 − 6x4 + 11x3 − x2 − 14x + 5 = 0.
They have given me a zero, so I'll use synthetic division and divide out 2 − i:
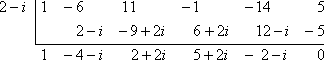
(You will probably want to use scratch paper for the computations required when doing complex division.)
What should I try next? I'll use the fact that, to arrive at a zero of 2 − i, the author of this exercise must have used the Quadratic Formula at some point, and the Quadratic Formula always spits out complex-valued answers in pairs. That is, you get the imaginary part (the part with the i in it) from having a negative inside the "plus or minus square-root of" part of the Formula. This means that, since 2 − i is a zero, then 2 + i must also be a zero. So I'll divide by 2 + i:
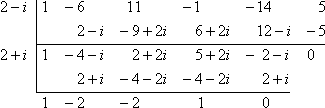
This leaves me with a cubic, so I'll need to find another zero on my own. (That is, I can't apply the Quadratic Formula yet.) I can use the Rational Roots Test to generate a list of potential zeroes, and a quick graph of y = x3 − 2x2 − 2x + 1 can help me narrow my search.
After checking the graph in my calculator, I decide that I will try x = −1:
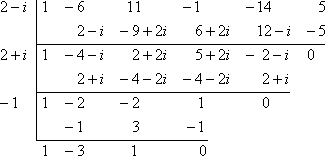
Now I'm down to a quadratic (namely, x2 − 3x + 1) which happens not to factor, so instead I'll apply the Quadratic Formula to get:
Then all the zeroes of x5 − 6x4 + 11x3 − x2 − 14x + 5 are given by:
In the examples above, I repeatedly referred to the relationship between factors and zeroes. In other lessons (for instance, on solving polynomials), these concepts will be made more explicit. For now, be aware that checking a graph (if you have a graphing calculator) can be very helpful for finding the best test zeroes for doing synthetic division, and that a zero remainder after synthetic division by x = b means that x − b is a factor of the polynomial. If you do not have access to a graphing calculator for helping you find the right zeroes to try, there are some tricks you can use.
For an explanation of why synthetic division works (and for information on a variant method which will work for non-linear divisors), look at the pdf titled "How Synthetic Division Works, or, The Madness Behind the Method", written by Walter Kehowski of Glendale Community College in Arizona.
© 2024 Purplemath, Inc. All right reserved. Web Design by 