Synthetic Division, Factors, and Zeroes
Purplemath
Given a polynomial, we often would like to find its x-intercepts, also called its zeroes, solutions, or roots.
These are the x-values that cause the polynomial to have a value of zero; graphically, these are the places where the graph of the polynomial crosses (or at least touches) the x-axis.
What is the relationship between factors and roots?
If a polynomial has a root at x = b, this tells us that the polynomial has a factor of x − b, and vice versa.
We can use long division to find factors of a polynomial, and then solve those factors (by setting them equal to zero) to find the polynomial's roots. But long division is a pain. So, instead, if we're lucky enough that the polynomial has linear factors, we can use synthetic division to find the zeroes, and then, if needed, we can work backwards to find the polynomial's factors.
- Use synthetic division to determine whether x = 1 is a zero of x3 − 1.
I will set up the synthetic division, and check to see if the remainder is zero. If the remainder is zero, then x = 1 is a zero of x3 − 1.
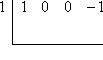
To do the initial set-up, note that I needed to leave "gaps" for the powers of x that are not included in the polynomial. That is, I followed the practice used with long division, and wrote the polynomial as x3 + 0x2 + 0x − 1 for the purposes of doing the division. If you forget to leave "gaps", your division will not work properly!
Step 1:
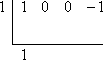
Step 2:
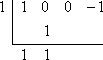
Step 3:
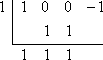
Step 4:
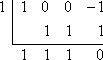
Since the last value in the bottom row is zero, then the remainder on this division is zero. Since the remainder is zero, then:
x = 1 is a zero of x3 − 1
They didn't ask but, since x = 1 is a zero of x3 − 1, then x − 1 is a factor. The bottom row of the synthetic division tells us what the other factor is; namely, x2 + x + 1. The polynomial x3 − 1 factors as:
(x − 1)(x2 + x + 1)
- Use synthetic division to find all the zeroes of x4 + x3 − 11x2 − 5x + 30.
Comparing the results of the Rational Roots Test to a quick graph, I decide to test x = 2 as a possible zero. I set up the divison:
...and here is the result:
Since the remainder is zero, then x = 2 is indeed a zero of the original polynomial.
To continue on and find the rest of the polynomial's zeroes, should I start over again with x4 + x3 − 11x2 − 5x + 30? Well, think about when you factor something like 72. After you divide a 2 out and get a 36, do you go back to the 72 to try the next factor, or do you see what will go into the 36? Of course, you try factors into the 36. It is simplest to follow the same procedure here. So I won't return to the original polynomial, but will instead see what divides into my result.
(Recall that synthetic-dividing out x = 2 is the same as long-dividing out x − 2, so the result has a degree that is one lower than what I started with. That is, to continue, I will be dealing not with the original fourth-degree polynomial x4 + x3 − 11x2 − 5x + 30, but with the third-degree result from the synthetic division: x3 + 3x2 − 5x − 15.)
Continuing, and again comparing the Rational Roots Test with a quick graph, I will try x = −3. Iet up the division:
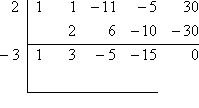
...and here is the result:
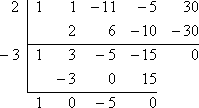
Since the remainder is zero, then x = −3 is a zero of the original polynomial. At this point, the final result is a quadratic, (x2 − 5), and I can apply the Quadratic Formula or other methods to get the remaining zeroes:
Then all the zeroes are:
The above example shows how synthetic division is most-commonly used: You are given some polynomial, and told to find all of its zeroes. You create a list of possibilities, using the Rational Roots Test; you plug various of these possible zeroes into the synthetic division until one of them "works" (divides out evenly, with a zero remainder); you then try additional zeroes on the resulting (and lower-degree) polynomial until something else "works"; and you keep going like this until you get down to a quadratic, at which point you use the Quadratic Formula or other methods to get the last two of the original polynomial's zeroes.
© 2024 Purplemath, Inc. All right reserved. Web Design by 