Solving Proportions: Similar Figures
Purplemath
Proportionality equations can be used to "solve" "similar figures".
What are "similar figures"?
"Similar" is a geometric term, referring to geometric figures (squares, triangles, etc) that are the same shape, but one of the pair of figures is larger than is the other.
For a mental picture of similar figures, think of what happens when you use the "enlarge" or "reduce" setting on a copier, or when you get an eight-by-ten enlargement of a three-by-five picture you really like, or, if you've used a graphics program, think about preserving the "aspect ratio" of an image that you're resizing. Each of these examples results in a pair of similar figures (or similar pictures, anyway).
How do you "solve" similar figures?
In the context of ratios and proportions, the point of similarity is that the corresponding sides of similar figures are proportional; that is, that the lengths of matching sides are proportional. So, given two similar figures, not all of whose sides are labelled with their lengths, you can create a proportionality equation mixing known and unknown information, and solve for the unknown value.
Note: For this process to work, the similar figures must have at least one pair of corresponding sides both of whose lengths is known. This pair will be your reference pair, forming one side of your proportionality equation.
For instance, look at the similar triangles ABC and abc below:
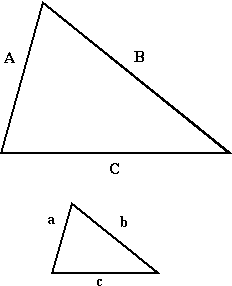
The "corresponding sides" are the pairs of sides that "match", other than for the enlargement or reduction aspect of their relative sizes. So A corresponds to a, B corresponds to b, and C corresponds to c.
Since these triangles are similar, then the pairs of corresponding sides are proportional. That is, A : a = B : b = C : c. In words, this tri-part equation says, "Big-A is to little-A as big-B is to little-B and as big-C is to little-C". This proportionality of corresponding sides can be used to find the length of a side of a figure, given a similar figure for which sufficient measurements are known.
- In the displayed triangles, the lengths of the sides are given by A = 48 mm, B = 81 mm, C = 68 mm, and a = 21 mm. Find the lengths of sides b and c, rounded to the nearest whole number.
I'll set up my proportions, using ratios in the form (big triangle length) ÷ (small triangle length), and then I'll solve the proportions. (By the way, you can set up your proportions as you like; there is no rule that says "bigger goes on top".)
Since they've only given me the length of side a for the little triangle, my reference ratio will be A : a.
First, I'll find the length of b. Here's my set-up:
(There is no requirement that you label things, as I did above with the initial fraction containing the words "big" and "small", but this can be very helpful in reminding yourself how you're wanting to set things up. It's a quick way of keeping yourself out of trouble.)
Filling in my known values, I get:
![48 / 21 = 81 / b: multiply across to get (81)(21); divide back by 48; d = [(81)(21)]/48](ratio/ratio39a.gif){kind=small}
(I'll need to remember to give the rounded-to-whole-number value for this side's length (in other words, I'll need to remember to round to "35") in my hand-in answer.)
Now that I've found one length, I will, by the same method, find the length of the remaining side, c.
![multiply across for (68)(21); divide back by 48; then c = [(68)(21)]/48](ratio/ratio41a.png){kind=small}
For my answer, I could just slap down the two numbers I've found, but those numbers won't make much sense without their units. Also, in re-checking the original exercise, I'm remindedthat I'm supposed to round my values to the nearest whole number, so "29.75", with or without units, would be wrong. The right answer is:
b = 35 mm, c = 30 mm
While I could have used the length I'd found for b for finding the length of c in the above exercise, I instead returned to the value of a. Why? Because it was a known-good "exact" value.
While the decimal value was in this case an exact value (that is, the value for b was not rounded), it's generally better to make a habit of returning to known-good values whenever you can. That way, when a decimal value has been rounded, you're ignoring the rounded derived value and returning to the exact original value.
This practice will help you avoid the potential for round-off errors.
- A picture measuring 3.5″ (that is, 3.5 inches) high by 5″ wide is to be enlarged so that the width will be 9″. How tall will the picture be?
The photo lab, when enlarging the original picture, will be maintaining the aspect ratio of the original; that is, the rectangles representing the outer edges of the original and enlarged pictures will be similar figures. Using this fact, I can set up a proportion and solve, using "h" to stand for the height value that I'm seeking:
![multiply 9 by 3.5 going across; divide by 5 hooking back; then h = [(9)(3.5)]/5](ratio/ratio43a.png){kind=small}
The height of the picture will be:
6.3 inches
In the first exercise above, the ratios were between corresponding sides, and the proportionality was formed from those pairs of sides. The ratios in the proportions contained fractions formed from the original large value divided by the new small value. In the second exercise above, the ratios were between the two different dimensions, and the proportionality was formed from the sets of dimensions. The ratios in the proportion contain fractions formed from the old height and old width, and from the new height and the new width.
For many exercises, you will be able to set up your ratios and proportions in more than one way. This is perfectly okay. Just make sure that you label things well, clearly define your variables, and set things up in a sensible and consistent manner. Doing so should help you dependably reach the correct solutions. If you're ever not sure of your solution, remember to plug it back into the original exercise, and verify that it works.
There is another topic, kind of an off-shoot of similar-figures questions, which you may encounter. It is based on the fact that, if two figures (or three-dimensional shapes) are similar, then not only are their lengths proportional, but so also are their squares (being their areas) and their cubes (being their volumes).
- Two rectangular prisms are similar, with one pair of corresponding lengths being 15 cm and 27 cm, respectively. (a) If the volume of the smaller prism is 2000 cm3, what is the volume of the larger prism? (b) If the area of one face of the larger prism is 243 cm2, what is the area of the corresponding side of the smaller prism?
A "rectangular prism" is just fancy geometrical talk for "a brick", so I know that I'm working with three-dimensional shapes. I am given that the shapes are similar, and I'm provided with two comparative lengths. This gives me my basic ratio:
This is the simplified (that is, reduced to lowest terms) linear ratio for the two prisms, and it's what I'll use for finding my answers for volume and surface area.
(a) To find the volume of the larger prism, I need to cube the linear ratio they gave me (that is, I need to cube the reduced fraction that I'd created when I'd put the two lengths into a ratio, above). Putting the values for the smaller prism in the tops of the ratios, this gives me:
This is the ratio I'll use for setting up my volume proportion:
![multiply across 2000 by 729; divide back by 125; then V = [(2000)(729)]/125](ratio/ratio57.png){kind=small}
Checking my units, I get an answer of:
(a) 11,664 cm3
(b) To find the surface area of the one side of the smaller prism, I need to square the linear ratio they gave me (that is, I need to square the reduced fraction created by putting the two lengths into a ratio). Putting the values for the smaller prism in the tops of the ratios, this gives me:
This is the ratio I'll use for setting up my area proportion.
![multiply across 243 by 25; divide back by 81; then A = [(243)(25)]/81](ratio/ratio59.png){kind=small}
Checking my units, I get an answer of:
(b) 75 cm2
© 2024 Purplemath, Inc. All right reserved. Web Design by 