Maximim / Minimum Geometry Word Problems
Purplemath
What are max/min geometry problems?
A special case of geometry word problems involves having to maximize or minimize some dimension, area, or volume of a geometric figure. This will involve your creating a model (that is, an equation) that turns out to involve a quadratic
Then you'll find the vertex of that quadratic, since the vertex will give the maximizing or minimizing value for your model.
- Find the largest possible rectangular area you can enclose, assuming you have 128 meters of fencing. What is the (geometric) significance of the dimensions of this largest possible enclosure?
I'll let the length be L and the width be w. I have 128 meters of fencing, so the perimter equation is:
2L + 2w = 128
Dividing by 2 to make things simpler, I get:
L + w = 64
Previously, they would have given me the perimeter and area and I would have had to find the length and width. This time, they told to find the area; in particular, they told me to find the *largest* area, given this perimeter. How do I do that?
Let's look at the area equation:
A = L × w
I can substitute for either one of these variables by solving the perimeter equation:
L + w = 64
L = 64 − w
I can plug this into the area equation:
A = (64 − w) × w
= 64w − w2
After substitution and simplification, my area equation has become a quadratic. I'm supposed to find the maximum, so I need to find the vertex. Since the above area equation is a negative quadratic, then it graphs as an upside-down parabola, and the vertex is the maximum.
There are a couple different ways of finding the vertex. I'll take the easy way. The equation of this quadratic, arranged in y = ax2 + bx + c format, is:
A = −w 2 + 64w
The vertex of a parabola is the point (h, k), where the maximizing value is at . In this case, this formula gives me:
To find the "k" part of the vertex — which is the maximum value for the area — all I do is plug 32 in for w:
k = −(32)2 + 64(32) = 1024
My points from this equation are (w, A) — that is, I plug in a width and figure out the area — so the h is the maximizing width and the k is the maximum area. So the answer for the maximum area is:
largest area: 1024 m2
I know that this maximum occurs when the width is 32 meters. Now I also need to find the length, because the original question asked about the "significance" of the dimensions. Since w = 32, then:
L = 64 − w
= 64 − 32 = 32
Then the length and width are the same: 32 meters. What do you call a rectangle that is as wide as it is long? A square. So the second part of the answer is:
The largest possible rectangular area is in the shape of a square.
Educators have started noticing that students have figured out the solution to the above exercise, just as a rule: "The rectangle with the largest area for a given perimeter will be a square" and, vice versa, "The rectangle with the shortest perimeter for a given area will be a square". So they've come up with new forms of the exercise; fortunately, the reasoning and general process are exactly the same.
- The riding stables has just received an unexpected rush of registrations for the next horse show, and quickly needs to create some additional paddock space. There is sufficient funding to rent 1200 feet of temporary chain-link fencing. The plan is to form two paddocks with one shared fence running down the middle. What is the maximum area that the stables can obtain, and what are the dimensions of each of the two paddocks?
To help me see what I'm doing, I first draw a picture:
The total area A for the two paddocks will obviously be A = Lw. The total length of fencing gives me the total "perimeter" (in quotes, because I'm also including that shared line down the middle, so this isn't the "regular" perimeter). Then:
P = 1200 = 2L + 3w
I can't do much with this, but what if I solve this for one of the variables, and then plug that into the "area" formula? Let's see...
1200 = 2L + 3w
1200 − 3w = 2L + 3w − 3w
1200 − 3w = 2L
Now I'll plug this into the area formula:
This is a negative quadratic, just like the previous exercise, and I'll find the maximum area in the same way: by finding the vertex. First, I'll find the maximizing value for the width:
So I will get the maximum area when the input (the width, in this case) has a value of 200. Reviewing my picture and equations, I see that the width should be 200 feet, the overall length should be 300 feet, and each paddock should then be 150 feet long.
maximum area: 60,000 sq ft
each paddock's area: 30,000 sq ft
paddock width: 200 ft
paddock length: 150 ft
shared side: 200 ft
In particular, note that the maximal area above is not a square!
Other ways of skewing the solutions away from squares, circles, or spheres is to include cost considerations, such as the material for the base of an open-topped box costing more (because it needs to be stronger) than the material for the sides. In other words, don't just assume that the neatest answer will be the correct answer. Do the actual math.
- An isosceles triangle has height 48cm and base 16cm, and has inscribed within it a rectangle, as shown below. Find the dimensions of the rectangle that minimize the shaded area between the rectangle and the triangle.
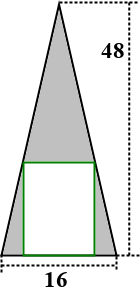
To set this up, I need to find an expression for the shaded area, and then I need to figure out how to make that as small as possible. I'll start by labelling.
Because the rectangle's bottom lies within the base of the triangle, then I know that the rectangle's vertical sides form right angles with the base of the triangle. Because the triangle is isosceles, I know that each half (that is, each portion on either side of the altitude line up the middle) of the triangle is the same. Also, the small shaded triangles at the bottom corners of the larger triangle are similar to half of the original triangle.
I'll label the base of one of the smaller triangles as b and the height of that triangle has h. The other smaller triangle will have the exact same dimensions. And, by subtraction, the height of the shaded triangle on top must be:
height: 48 − h
base: 16 − 2b
So I have the following:
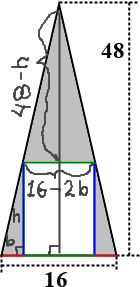
The shaded areas are then given by:
each small corner: ½bh
top triangle: ½(16 − 2b)(48 − h)
Adding together the two small corner triangles and the bigger one on top, the total area of shading is given by:
2(½bh) + ½(16 − 2b)(48 − h)
bh + (8 − b)(48 − h)
But this area expression has too many variables. I need to get rid of one of them. Looking at one of the bottom-corner triangles, I can use the similarity of this corner triangle and half of the surrounding triangle (which, being half of the isosceles triangle, has a base length of 8 units) to get:
I can use this to replace b in my "area to be minimized" expression:
bh + (8 − b)(48 − h)
This is a positive quadratic in h, which means that it graphs as an upward-opening parabola, so the minimizing point will be at the vertex. I can use the formula to find the minimizing value of h:
This is the minimizing value of the height h of the rectangle. The base of the rectangle is then . Looking back at the exercise, while the picture contained no units, the problem statement did: centimeters. I will need to include that unit in my answer.
height: 24 cm
base: 4 cm
By the way, yes, this could have been stated as a maximization exercise, by asking for the dimensions of the largest rectangle that would fit inside the given triangle. The largest rectangle would leave the smallest area that could be shaded.
© 2024 Purplemath, Inc. All right reserved. Web Design by 