Recursive Sequences
Method of Common Diff'sExamples of Common Diff'sGeneral ExamplesMore ExamplesNon-Math SequencesMore Non-Math
Purplemath
What is a recursion?
A recursion is a list of values in which the later values are built from the earlier values. A recursive sequence will have one or more "seed" values, because you have to have something to start with, and then it will have a rule for building the rest of the terms in the list.
Content Continues Below
Because the rule for a given list relates specific earlier values to the next value that you need to build, you can only find, say, the twentieth value by building the third, then the fourth, then the fifth,..., then the eighteenth, and then the nineteenth. Only then can you find the twentieth. So recursions can be a bit of a pain.
(Sometimes a recursive formula can be converted to a formula in terms only of the index n — this new formula is called the "closed form" of the recursion — but finding that closed form can be tricky.)
Let's take another look at the last sequence on the previous page:
- Find the next term in the following sequence: 1, 4, 8, 13, 19, 26,...
Our formula ended up being , from which we computed the seventh value, 34.
This formula was a bit messy, what with the fractions. But the row of first differences points out a simpler rule. Each next term was gotten by adding a growing amount to the previous term.
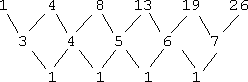
To get the second term, they added 3 to the first term; to get the third term, they added 4 to the second term; to get the fourth term, they added 5 to the third term; and so on. The rule, in mathematical vocabulary, is:
To get the n-th term, add n+1 to the (n−1)-th term.
Typically, the n-th term of a recursion is referred to as an. In table form, the above rule looks like this:
n |
an |
change |
an+1 |
|---|---|---|---|
1 |
1 |
+3 |
4 |
2 |
4 |
+4 |
8 |
3 |
8 |
+5 |
13 |
4 |
13 |
+6 |
19 |
5 |
19 |
+7 |
26 |
6 |
26 |
+8 |
34 |
This sort of sequence, where you get the next term by doing something with some previous terms, is a recursive sequence. On the previous page, we had come up with a polynomial formula (that is, with a closed form expression) for the sequence. Finding the closed form of a recursion is often not possible (or at least is not reasonable), which is why you need to keep them in mind as a different type of sequence.
Affiliate
Advertisement
What is the Fibonacci sequence?
The Fibonacci (fibb-uh-NAH-chee) sequence is probably the most famous of the recursive sequences. Its first two terms are seed values; then the rule for all the later terms is to add the previous two terms:
a1 = 0
a2 = 1
an = an−1 + an−2 for n > 2
(The subscripts indicate which term you're on: a1 is the first term, a2 is the second term, an is the n-th term, and an−1 and an−2 are the terms that are one before and two before an, respectively.)
That is, the first two terms are each defined to have the values of 0 and 1, respectively. These are the seed values of the Fibonacci sequence. Then the third term is the sum of the previous two terms, so:
a3 = 0 + 1 = 1
Then the fourth term is the sum of the second and the third, so:
a4 = 1 + 1 = 2
And so forth. The first few terms of the Fibonacci sequence are:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377,...
While recursive sequences are easy to understand, they are difficult to deal with. Why? Because, in order to find, say, the thirty-nineth term in this sequence, you first have to find terms a1 through a38. There isn't a formula into which you can simply plug n = 39 and get your answer. (Well, there is, but its development is likely far beyond anything you've yet been trained to do.) For instance, if you try to find the differences for some early terms of the Fibonacci sequence, you'll get this:
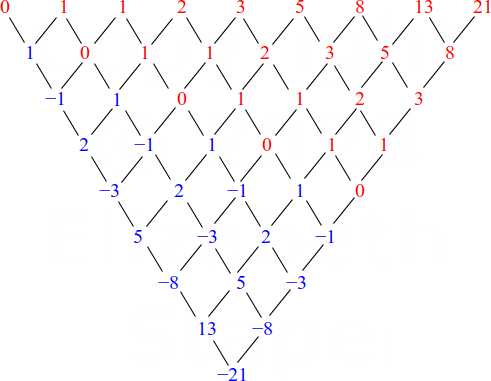
As you can see, you're not going to get a row of differences where all the entries are the same. However, you should notice that the sequence repeats itself in the lower rows, but shifted over to the right. And, in the beginning of each lower row, you should notice that a new sequence is starting: first 0; then 1, 0; then −1, 1, 0; then 2, −1, 1, 0; and so on. This is characteristic of "add the previous terms" recursive sequences. If you see this kind of behavior in the rows of differences, you should try finding a recursive formula.
(This table of common differences would generate a degree-eight polynomial that can be guaranteed to fit only these first nine terms. The polynomial won't give the Fibonacci sequence in its entirety.)
Content Continues Below
It is, in general, fairly difficult to figure out the formulas for recursive sequences, so usually they'll give you fairly simple ones of the "add a growing amount to get the next term" or "add the last two or three terms together" type:
- Find the next number in the sequence: 3, 2, 5, 7, 12, ...
Fortunately for me, the second term is smaller than the first, which grabs my attention and kind of highlights the fact that, after the first two terms (which must be the seed values), each following term is the sum of the two previous terms. In other words, I'm pretty sure that this is what I'm seeing:
n |
an−2 |
an−1 |
adding |
an |
|---|---|---|---|---|
1 |
|
|
|
3 |
2 |
|
3 |
|
2 |
3 |
3 |
2 |
3+2 |
5 |
4 |
2 |
5 |
2+5 |
7 |
5 |
5 |
7 |
5+7 |
12 |
If I'm right about the rule, then the next term would be:
7 + 12 = 19
By the way, the differences look like this:
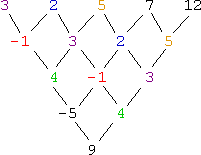
Note how the sequence terms are repeated in lower rows, but shifted to the right, and how the new sequence terms are entering from the left.
- Find the next term in the sequence: 1, 2, 2, 4, 8, 11, 33, 37, 148, ...
This one is harder (and is not, strictly speaking, recursive). Take a look at the differences:
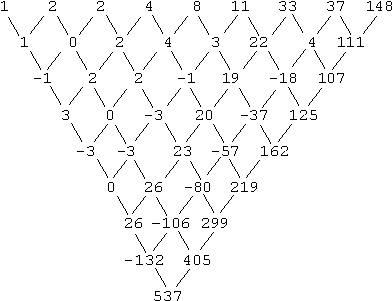
As you can see, I'm not getting nothing useful from this table of differences. (I mean, yeah; I could find a degree-8 polynomial that goes through these values, but — yeesh!) The reason for this unhelpfulness is that the sequence's rule in this instance is not consistent:
n |
an−1 |
rule |
an |
|---|---|---|---|
1 |
|
1 |
|
2 |
1 |
+1 |
2 |
3 |
2 |
×1 |
2 |
4 |
2 |
+2 |
4 |
5 |
4 |
×2 |
8 |
6 |
8 |
+3 |
11 |
7 |
11 |
×3 |
33 |
8 |
33 |
+4 |
37 |
9 |
37 |
×4 |
148 |
Then the next term will be "add five":
148 + 5 = 153
Affiliate
As the above example shows, even the table of differences might not help with a (pseudo-) recursive sequence. But don't be discouraged if it takes a while to find a formula or a pattern. If the sequence is mathematical, then it should be possible, eventually, to find some sort of an answer. The next page demonstrates some solutions.
URL: https://www.purplemath.com/modules/nextnumb3.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()




