The Rule for Matrix Multiplication
Purplemath
In the course of multiplying one matrix by another, we have seen that matrix multiplication is accomplished by multiplying, entry-wise, the rows of the left-hand (that is, of the first) matrix by the columns of the right-hand (that is, of the second) matrix, and then summing the products to get the entries of the product matrix.
Content Continues Below
But this entry-wise multiplication requires that the number of entries in the rows of first matrix is the same as the number of entries in the columns of the second matrix. Does that mean that some matrices cannot be multiplied together?
Advertisement
What is the rule for which matrices can be multiplied together?
Affiliate
In order for two matrices to be able to be multiplied together, the number of columns in the left-hand matrix must be the same as the number of rows in the right-hand matrix. Put another way, the number of entries in the rows of the left-hand matrix must be the same as the number of entries in the columns of the right-hand matrix.
Just as with adding matrices, the sizes of the matrices matter when we are multiplying. For matrix multiplication to work, the columns of the second matrix have to have the same number of entries as do the rows of the first matrix.
Let's take another look at the matrix multiplication from the previous page:
Affiliate
If, using the above matrices, B had had only two rows, its columns would have been too short to multiply against the rows of A. Under this condition, the matrix product AB would not have existed; the product would have been "undefined" (that is, it would not make any mathematical sense).
Likewise, if B had had, say, four rows, or alternatively if A had had two or four columns, then AB again would not have existed, because A and B would not have been the right sizes.
In other words, for AB to exist (that is, for the very process of matrix multiplication to be able to function properly), A must have the same number of columns as B has rows; looking at the matrices, the rows of A must be the same length as the columns of B.
Content Continues Below
You can use this fact to check quickly whether a given multiplication is defined (and you *will* be asked). Write the product in terms of the matrix dimensions. In the case of the above example, A is 2×3 and B is 3×2, so the product AB, stated in terms of the matrice's dimensions, is (2×3)(3×2).
The middle values match, so the matrix product makes sense, within the rules and definitions:
...so the multiplication is defined. As you can see, the matrix AB, being the product matrix, is a 2×2 matrix. You can also see this on the dimensions:
Using this sizing information, you can see that the product matrix BA must be a different matrix from the product AB, because its dimensions aren't even the same:
The product BA is defined; that is, the product conforms to the rules that allows us to do the multiplication. But the product's dimensions, when the matrices are multiplied in this order, will be 3×3, not 2×2 as was AB.
In particular, matrix multiplication is *not* commutative. You cannot switch the order of the factors (that is, the matrices in the product) and expect to end up with the same result. For matrix multiplication, AB no longer equals BA.
(You should expect to see a concept question relating to this fact on your next test.)
You can use the Mathway widget below to practice finding the dimensions of a matrix. (Or skip the widget and continue with the lesson.) Try the entered exercise, or type in your own exercise. Then click the button and select "Find the Dimensions" to compare your answer to Mathway's.
Please accept "preferences" cookies in order to enable this widget.
(Click "Tap to view steps" to be taken directly to the Mathway site for a paid upgrade.)
- Given the following matrices, find the product BA.
![A = [[ 1 0 -2 ][ 0 3 -1 ]] , B = [[ 0 3 ][ -2 -1 ][ 0 4 ]]](matrices/mult06.gif)
The multiplication works the same way as the previous problem, going across the rows and down the columns. I won't try drawing my hands again, but you can see the computations in the colors below:
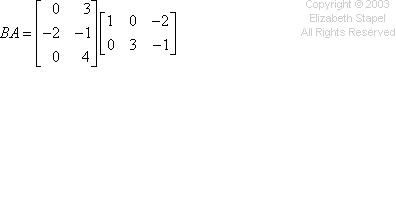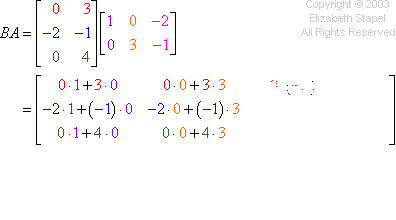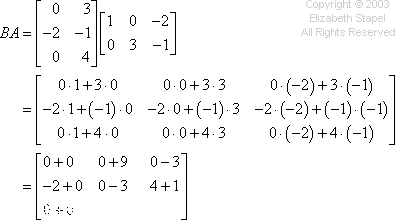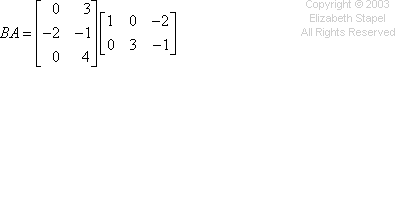
Then my answer is:
![BA = [[ 0 9 3 ][ -2 -3 5 ][ 0 12 -4 ]]](matrices/mult09.gif)
- Find CD and DC, if they exist, given that C and D are the following matrices:
C is a 3×2 matrix and D is a 2×4 matrix. Before I attempt the multiplication, first I'll look at the dimension product for CD:
So the product CD is defined (that is, I can do the multiplication); also, I can tell that I'm going to get a 3×4 matrix for my answer. Here's the multiplication:
However, look at the dimension product for DC:
Since the inner dimensions don't match, I can't do the multiplication. The columns of C aren't the same length as the rows of D; the columns of C are too short, or, if you prefer, the rows of D are too long.
So my answer is:
DC is not defined.
URL: https://www.purplemath.com/modules/mtrxmult2.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()




