Minors, Cofactors, and Some Rules
Purplemath
In the last example on the previous page, we found the determinant by taking the 4-by-4 determinant down to 3-by-3 determinants. But technically, you're supposed to go down to 2-by-2 determinants when you expand along a row or column. That is, the cofactors should have been computed using *way* more steps.
Content Continues Below
To see how this works (that is, to see how painful a process this is) let's go across the first row again. The first cofactor should "properly" have been computed like this:
a1,1 entry of det(A) selected:
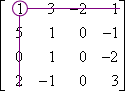
minor M1,1:
By crossing out a row and column of the original determinant, a new determinant is formed. Call this new determinant D. To find the value of D, let's expand along its first row.
d1,1:
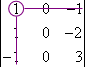
cofactor: (+1)(0 − 0) = 0
d1,2:

cofactor: (−1)(3 − 2) = −1
d1,3:

cofactor: (+1)(0 − 0) = 0
Then the value of D is:
1(0) + 0(−1) + −1(0) = 0
And then the first cofactor is:
C1,1 = (−1)2D = (1)(0) = 0
And that's just *one* cofactor; we still have three more to go!
Affiliate
Using this methodology, all determinants can be boiled down to finding 2-by-2 determinants. But—
Since you know how to find 3-by-3 determinants, there is no need to go all the way down to 2-by-2's — unless the instructions specifically require that you do so. I hope they don't, cuz that's just mean.
As you've seen, having a "zero-rich" row or column in your determinant can make your life a lot easier. Since you'll get the same value, no matter which row or column you use for your expansion, you can pick a zero-rich target and cut down on the number of computations you need to do.
Of course, not all matrices have a zero-rich row or column. But there is a rule that can help:
If you add a multiple of one row (or column) to another row (or column), the value of the determinant will not change.
In other words, you can do this row operation (or column operation) on determinants, using this to create a row (or column) with lots of zeroes, and you'll still get the right value for the determinant.
(You can also just multiply rows and columns — without the adding to another row or columns — or switch rows or columns, but those operations will change the determinant's value. The changes are annoying to keep track of, so I try only to do the row- or column-addition operation.)
Content Continues Below
- Find the following determinant by expanding along the row or column of your choice:
No particular row or column looks any better (that is, any easier) to expand along than the others. I think I'll do some row- (and column-) operations first, to get some more zeroes in the determinant. And, because the first column contains a leading 1 (in the third row), I think I'll start by using that leading 1 to create some zeroes in the first and fourth rows:

Ah! That's much nicer. Now I can expand along the first row or along the first or second column, and my computations will be much easier than if I'd stuck with the original determinant.
I think I'll go down the first column. The only cofactor I actually need to compute is C2,1, which I'll multiply by the entry a2,1:
Then the value of the determinant is −15.
I mentioned that there are other ways to manipulate determinants. These "other ways" are to do the other row operations that you're used to (and also apply these rules to the columns). However, the other operations will change the value of the determinant. These other rules are:
If you interchange (that is, if you switch) two rows (or columns) of a matrix A to get the new matrix B, then det(A) = −det(B).
If you multiply a row (or a column) of A by some numerical value "k" to get the new matrix B, then .
In other words, if you multiply a row (or column) without adding it to another row (or column), then you have to keep track of that multiplier, and divide it off in the end. And if you switch two rows (or columns), you have to change the sign on the answer in the end.
The trouble with these two additional rules is, of course, that it's crazy-easy to lose track of what all you multiplied by, how many times you've switched columns, etc, which is why I try to stay away from these operations.
But if you're very careful, these other operations can be handy. Returning to that last determinant (above), look at these row switches:

I did two row switches, so I've got two sign changes, which takes me right back to the original sign for the determinant. And now, expanding down the first column, I get:
Advertisement
Did you see that? By manipulating the determinant into upper-triangular form (where everything below the diagonal is zero), the value of the determinant turned out to be the product of the values on the diagonal (times the two sign changes, which cancel each other out in this case).
Affiliate
Multiplying along the diagonal is much simpler than doing all the minors and cofactors. Given the opportunity, it is almost always better to do row operations and only then do the expansion along rows or columns. Unless you have an instructor who absolutely insists that you expand determinants in their original form, try to do some row (and column) operations first. If you're having to do determinants by hand, doing operations first will make your life so much easier.
We've already seen some determinant rules. Two more are as follows:
For matrices A and B, det(AB) = det(A)det(B).
If A is n-by-n, then det(kA) = kndet(A).
We have also seen that the determinant of a triangular matrix C is just the product of the elements on the diagonal. This tells us that the determinant of the identity matrix I is det(I) = 1. And this leads to a sometimes-useful result:
Any invertible matrix A has an inverse matrix A−1 such that (A)(A−1) = (A−1)(A) = I. Since det(AA−1) = det(I) = 1, then, whatever the value of det(A) is, the value of det(A−1) must be the reciprocal of det(A). For instance, if det(A) = 2/3, then det(A−1) = 3/2, so det(AA−1) = det(A)det(A−1) = (2/3)(3/2) = 1 = det(I).
But what if A isn't invertible? Think about it: What number has no reciprocal? The number zero. The only value for det(A) which won't allow for A to be invertible is zero. From this we get the following rule:
If a matrix A has no inverse, then det(A) = 0, and vice versa.
You may be asked at some point to "determine if the following matrix is invertible by using determinants". The question will be asking you to remember the above rule, and to see if the determinant is zero or not. You will not be expected actually to find the inverse.
If you're not going much further in mathematics, you may be able to get away with having your calculator do most or all of your determinant computations for you. But if you're planning on going on (for instance, to differential equations or linear algebra, or computer programming), then make sure you learn how to do determinants by hand. You will almost certainly need the skill.
(If you'd like to see proofs of some of these determinant rules, give Ohio State's online linear-algebra course [link] a try.)
URL: https://www.purplemath.com/modules/minors2.htm
You can use the Mathway widget below to practice finding determinants. Try the entered exercise, or type in your own exercise. Then click the button and select "Find the Determinant" to compare your answer to Mathway's.
Please accept "preferences" cookies in order to enable this widget.
(Click "Tap to view steps" to be taken directly to the Mathway site for a paid upgrade.)
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()




