Solving Rational Inequalities
Purplemath
Solving rational inequalities works much like solving polynomial inequalities, in that the rational expressions will often have many factors which will split the number line into many intervals. However, the important difference for rational inequalities is that, by definition, there will be factors in the denominator, which can cause division by zero.
Content Continues Below
So the basic process will be the same, but you'll need to take extra care with the denominators.
How do you solve rational inequalities?
To solve rational inequalities, follow these steps:
Affiliate
- Move terms, as necessary, to isolate the rational expression on one side of the inequality symbol, with zero on the other side.
- Simplify the rational expression, as necessary, to get one fraction (rather than added terms).
- Factor the numerator and denominator completely.
- Solve each factor to find the zeroes.
- Use the zeroes to split the number line into intervals. (Remember that zeroes in the denominator cannot be included in any solution, even if the inequality is an "or equal to" inequality, because you can never divide by zero.)
- Find the solution intervals by using the Test Point Method or the Factor Method.
Using the Test Point Method to test the intervals is generally time-consuming and error-prone. So I would recommend using the Factor Method, since you'll have the factors already anyway.
- Solve
First off, I have to remember that I can't begin solving until I have the inequality in "= 0" format. So I'll subtract the 2 over to the left-hand side:
Now I need to convert to a common denominator:
...and then I can simplify:
So the two factors of this rational expression are −x + 6 and x − 3. Note that x cannot equal 3, or else I would be dividing by zero, which is not allowed.
The numerator's factor, −x + 6, is positive for:
−x + 6 > 0
6 > x
x < 6
The other factor, x − 3, is positive for:
x − 3 > 0
x > 3
I need to remember that x cannot actually equal 3, so this endpoint can not be included in any solution interval — even though this is an "or equal to" inequality — because I can't divide by zero.
From my inequality endpoints, I see that my intervals are:
(−∞, 3), (3, 6], [6, +∞)
Affiliate
Advertisement
I have used square brackets at the 6 to remind me that 6 can be included in the solution; the parenthesis at 3 remind me that 3 cannot be included.
Using the Test-Point Method, I would pick a point in each interval and test for the sign on the result. I could use, say, x = 0, x = 4, and x = 7.
Using the Factor Method, I do my grid. I draw the number line aross the bottom of my grid, draw rows for each of the factors, draw vertical lines at the interval endpoints which split the number line into its intervals, and leave the top empty for the signs of the rational expression on each interval. My grid looks like this:
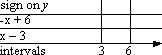
In each factor's row, I fill in the signs of the factors on each of the intervals:
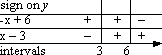
Then I count the "minus" signs in each column to find the sign of the rational expression on that column's interval. I put that interval's sign in the top row:
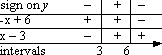
Checking the original exercise, I am reminded that I am needing the intervals where the rational expression is negative. So my solution is all x's in the following intervals:
(−∞, 3), [6, +∞)
A quick graph can serve to confirm the algebra:
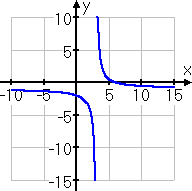
Content Continues Below
- Solve
Everything is already over on one side of the inequality, combined, and factored, so this will be pretty easy to do. I'll start with solving the various factors:
x + 3 > 0 ⇒ x > −3
x − 4 > 0 ⇒ x > 4
x − 1 > 0 ⇒ x > 1
x + 2 > 0 ⇒ x > −2
Now I can draw my factor table:
Checking the original exercise, I see that I need the intervals where the rational expression is positive. I need to remember that, though this is an "or equal to" inequality, I *cannot* include the zeroes x = −2 and x = 1, because doing so would cause division by zero.
So my solution intervals are:
(−∞, −3], (−2, 1), [4, +∞)
A quick graph confirms the solution:
![graph of y = [(x+3)(x−4)]/[(x−1)(x+2)]](ineqsolv/rtnl13.png)
URL: https://www.purplemath.com/modules/ineqsolv4.htm
You can use the Mathway widget below to practice solving rational inequalities. Try the entered exercise, or type in your own exercise. Then click the button and select "Solve the inequality for x" to compare your answer to Mathway's.
Please accept "preferences" cookies in order to enable this widget.
(Click "Tap to view steps" to be taken directly to the Mathway site for a paid upgrade.)
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()




