Solving Rational Inequalities

They've already put this inequality into (one rational expression) with (zero) on the other side. So I can start with factoring everything:

This polynomial fraction will be zero wherever the numerator is zero, so I'll set the numerator equal to zero and solve:

The fraction will be undefined wherever the denominator is zero, so I'll set the denominator equal to zero and solve:

These four values, −4, −2, −1, and +4, divide the number line into five intervals, namely:

I could use "test points" to find the solution to the inequality, by picking an x-value in each interval, plugging it into the original rational expression, simplifying to get a numerical answer, and then checking the sign, but that process gets long and annoying (and is prone to errors), so I'll use the easier and faster factor-table method instead.

My factor table looks like this:

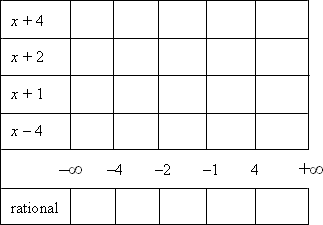
My table has one row for each factor, a row for the number line, and a row for the rational expression. Each row is split into columns, with each column corresponding to one of the intervals on the number line.

The sign of the overall rational expression is a result of the signs of its various factors, so I need to find where each factor is positive:

Now I can put "plus" signs on the intervals in each row where that row's factor is positive:

Wherever a factor isn't positive, it's negative, so I'll put "minus" signs in the remaining entries of each row:

I know that the product of an even number of "minus" signs is a plus; the product of an odd number of "minus" signs is a minus. So, by multiplying the signs down the columns (or just counting up the minusses), I get the overall sign of the rational expression on each interval:

Then the rational is positive on the intervals (−∞, −4), (−2, −1), and (4, +∞).

Looking back at the original exercise, this is an "or equal to" inequality, so I need to consider the interval endpoints, too.

If this were a polynomial inequality, I could just throw all the interval endpoints into the solution, and I'd be done. For rational expressions, though, I have to be careful not to include any x-values that would cause division by zero.

The intervals' endpoints are −4, −2, −1, and 4. I can include −2 and −1 in the solution, because they just make the expression equal to zero by making the numerator zero. But plugging −4 or 4 into the rational expression would cause division by zero, making the rational expression undefined, so I can't include these values in the solution.

Then my full solution is:

x < −4, −2 ≤ x ≤ −1, and x > 4