Solving Polynomial Inequalities: The Method
Purplemath
Solving polynomial inequalities relies on the fact that polynomials are continuous. In practical terms, this means that the graph of a polynomial is one unbroken line. That line may curve up and down a bit, but it never splits into pieces.
The zeroes of a polynomial are where the polynomial's graph touches or crosses the x-axis.
How does continuity help solve polynomial inequalities?
Because polynomials are continuous (that is, always-connected) curves, they will have the same sign between consecutive zeroes. In other words, between two consecutive x-intercepts, the curve will be always above the x-axis, or else always below. The polynomial's curve can't jump the axis between zeroes, because that curve is continuous.
Picture it this way: Consider two consecutive zeroes of a polynomial; that is, consider two spots, one right after the other, where that polynomial's graph touches or crosses the x-axis. Because the polynomial is continuous, then the graph is either above the x-axis for the entire length of the interval between the two consecutive places where it's at the axis, or else it is below the axis for the entire length.
In particular, the graph doesn't stop somewhere above the x-axis and then pick up again below the x-axis. Because the curve is one connected piece, it will be either above or else below the x-axis for the entire interval between two consecutive zeroes. That is, the polynomial's value will be either always positive (because it's above the x-axis) or else always negative (because it's below the x-axis) between any two consecutive x-intercepts.
This nice behavior on the part of polynomials leads to a quick method of solving simpler polynomial inequalities.
How do you solve simple polynomial inequalities? (graph method)
To solve inequalities involving simple polynomials (such as quadratics or cubics, and no repeated factors), work with what you know about the shapes of graphs.
- Isolate the polynomial on one side of the inequality symbol, with zero on the other side.
- Factor the polynomial completely.
- Use the zeroes of these factors to split the number line into intervals.
- Picture in your head the shape of the polynomial. For instance, a quadratic polynomial's shape will be a parabola.
- Pick the intervals where the graph corresponds to the inequality's symbol. For instance, if you are being asked to find where the polynomial is "greater than zero", then pick the interval(s) where the polynomial's graph is above the x-axis.
Here's an example of solving a simpler polynomial inequality:
- Find the solution: (x + 4)(x − 2)(x − 7) > 0
Since they've already factored this polynomial, much of my work is already done. So I'll go straight to finding the zeroes:
x + 4 = 0 ⇒ x = −4
x − 2 = 0 ⇒ x = 2
x − 7 = 0 ⇒ x = 7
These three zeroes divide the x-axis into four intervals:
(−∞, −4), (−4, 2), (2, 7), (7, +∞)
I need to figure out on which of these intervals the polynomial's graph is above the x-axis. If I'd multiplied the factors, I'd have ended up with a positive cubic polynomial, and I know what such a cubic looks like: it starts down on the left, comes up toward the axis, and eventually zooms upward on the right, with a bit of flexure in the middle, something like this:
From this knowledge, I know that the polynomial will be above the axis (that is, it will be "greater than zero") only on the second and fourth interval, so I can go straight to the solution:
(−4, 2), (7, +∞)
I can verify my solution from the polynomial's graph:
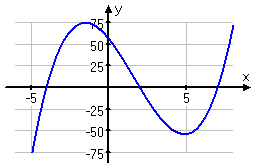
(Yes, you can cheat with a graphing calculator. But only cheat on polynomials that you can picture in your head, in case you're asked to "justify" your answer.)
As you can see, being familiar with polynomials and their shapes can make your life simpler for some of these problems.
But what if you haven't learned about their shapes, or if the polynomial is more complicated, or if you have to "show your reasoning"? Your book probably prattled on about "test points", but that method requires a lot of error-prone computation, so I prefer an easier method; namely, the factor-table method.
How do you solve polynomial inequalities? (table method)
To solve a polynomial inequality by the table method:
- Isolate the polynomial on one side of the inequality symbol, with zero on the other side.
- Factor the polynomial completely.
- Use the zeroes of these factors to split the number line into intervals.
- Set each factor "greater than zero" and solve, to find on which interval each factor is positive or negative.
- Create a factor table, and fill it with the signs for each factor on each interval.
- Count up "minus" signs to determine the polynomial's sign on each interval.
- Choose the intervals that satisfy the original inequality.
I'll re-work the above example exercise, this time using the factor-table method.
- Find the solution: (x + 4)(x − 2)(x − 7) > 0
The factors give me the zeroes of the polynomial, and the zeroes give me the following intervals of positivity and negativity:
(−∞, −4), (−4, 2), (2, 7), (7, +∞)
I just need to figure out on which invervals each factor is positive, and on which they're negative. Then I'll roll them all together, because the sign on the polynomial is the product of the signs on its factors.
I've got three factors, so I'll draw up a table of factors with the intervals marked off:
This table has a row for each of the factors, a row for the number line, and a row for the polynomial. Each row is divided into columns, with each column corresponding to an interval between zeroes on the number line.
Now I'll figure out where each factor is positive. (Each factor will be negative wherever it isn't positive.)
x + 4 > 0 ⇒ x > −4
x − 2 > 0 ⇒ x > 2
x − 7 > 0 ⇒ x > 7
I'll mark in the table the intervals where each of the factors is positive:
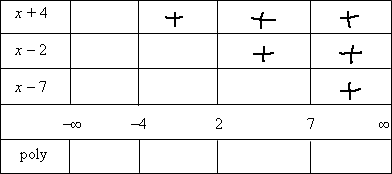
...and then I'm mark the factors as being negative everywhere else:
The factors multiply together to create the polynomial; the signs of the factors multiply together to give the sign of the polynomial. So I'll multiply the signs of the factors on each interval to find the overall sign of the polynomial on that interval:
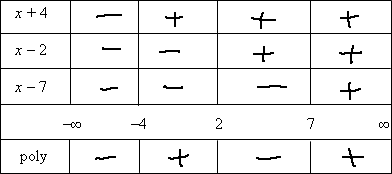
In the first interval, from negative infinity to −4, there were three "minus" signs, and the product of three negatives is a negative; I'll put a "minus" in the box for the interval (−∞, −4).
In the second interval, from −4 to 2, there were two "minus" signs, and the product of two negatives is a positive; I'll put a "plus" sign in the box for the interval (−4, 2).
In the third interval, from 2 to 7, there is just one "minus;" sign, so the polynomial here is negative; I'll put a "minus" sign in the box for the interval (2, 7).
In the fourth interval, from 7 to infinity, there are no "minus" signs, so the polynomial here is positive; I'll put a "plus" sign in the box for the interval (7, +∞).
Now I can read the solution directly from the table. Checking back with the original exercise, I need the intervals where the polynomial is positive, so I'll pick the intervals that have a "plus" sign in them on the bottom row of my table:
(−4, 2), (7, +∞)
In my experience, the easiest solution method for polynomial inequalities is to use what you know about polynomial shapes, but the shape isn't always enough to give you the answer. And the test-point method from your book will give you the answer *eventually*, but it can be a lot of work and is subject to calculation errors.
On the other hand, the factor-table method is quicker than test points and, since no computations are involved, you're less likely to make a mistake. So unless your instructor insists that you use the test-point method, try to learn the factor-table method. It'll make your life a lot easier.
© 2024 Purplemath, Inc. All right reserved. Web Design by 