Examples of Solving Quadratic Inequalities
Purplemath
What is the first step in solving quadratic inequalities?
The first step in solving quadratic inequalities is to isolate the quadratic's terms on one side of the inequality symbol, with zero, and only zero, on the other side.
If the inequality has polynomial terms on each side of the inequality, then you'll need to move some stuff around, to get started.
How do you solve quadratic inequalities, step-by-step?
To solve a quadratic inequality, follow these steps:
- Isolate the quadratic; in other words, move all the terms to one side of the inequality symbol, leaving zero on the other side.
- Factor (or apply the Quadratic Formula) to solve for the zeroess (that is, the x-intercepts) of the quadratic.
- Use these zeroes to split the number line into intervals.
- Picture (in your head, or in your graphing calculator) the parabola that corresponds to the quadratic.
- If the inequality is "greater than", then pick the intervals where the parabola is above the x-axis; if the inequality is "less than", then pick the intervals where the parabola is below the x-axis.
(Or, if your instructor insists, or if you prefer, pick "test points" in each interval to determine the sign on each interval; then pick the intervals that match the inequality. The test-point method would then replace steps 4 and 5 above.)
- Solve 2x2 + 4x ≥ x2 − x − 6.
This inequality has one quadratic being greater than another quadratic. I could try working with the two associated functions, y1 = 2x2 + 4x (shown in green on the graph below) and y2 = x2 − x − 6 (shown below in blue).
Here's the graph:
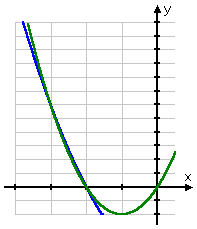
As you can see, this graph is not particularly helpful. I really can't tell *exactly* where the two lines cross over each other, so intervals are hard to pin down.
On the other hand, if I start properly by isolating the quadratic, my life will be much simpler.
2x2 + 4x ≥ x2 − x − 6
2x2 + 4x − x2 + x + 6 ≥ 0
x2 + 5x + 6 ≥ 0
This last inequality is simpler to deal with because now all I have to do is find where x2 + 5x + 6 equals zero (which is easy) and then pick the correct intervals based on just the one parabola (which is also easy).
In other words, it is simpler to compare one parabola with the x-axis than it is to *attempt* to compare two parabolas with each other. But the solution to the simpler one-parabola inequality will be the same as the solution to the original two-parabola inequality, so I'll work with the simpler case.
The zeroes (that is, the x-intercepts) of the isolated quadratic are at:
x2 + 5x + 6 = 0
(x + 2)(x + 3) = 0
x = −2 or x = −3
These two intercepts split the number-line into three intervals, namely:
x ≤ −3
−3 ≤ x ≤ −2
x ≥ −2
On which of these three intervals is y = x2 + 5x + 6 above the x-axis? Since this positive quadratic graphs as a right-side-up parabola, then the quadratic is above the axis on the ends:
So the solution is:
x ≤ −3 or x ≥ −2
- Solve x2 + 2x − 8 ≤ 0.
The quadratic is already isolated on the left-hand side of the inequality, so I can go straight to finding the zeroes:
x2 + 2x − 8 = 0
(x + 4)(x − 2) = 0
x = −4 or x = 2
These x-intercepts split the number line into three intervals:
x < −4
−4 < x < 2
x > 2
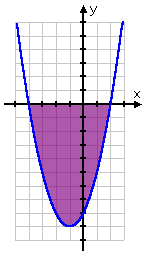
Since this is a "less than" inequality, I need the intervals where the parabola is below the x-axis. Since the graph of y = x2 + 2x − 8 is a right-side-up parabola, the graphed line is below the x-axis on the interval in the middle (that is, on the interval that's between the two intercepts).
Since this is an "or equal to" inequality, the boundary points of the intervals (that is, the x-intercepts themselves) are included in the solution.
So my answer is:
−4 ≤ x ≤ 2
You can check my answer from the graph:
Can you use the Quadratic Formula for solving quadratic inequalities?
When a quadratic won't factor (or if the coefficients are so large that factoring might turn out to be time-consuming), you can always plug the quadratic into the Quadratic Formula. The Quadratic Formula will spit out the locations of the x-intercepts, and thus tell you what are the inequality's intervals. For graphing purposes, use the decimal approximation of any zeroes with square roots in them; for writing your intervals, though, always use the exact form.
- Find the solution: x2 + 7 < 6x. State your answer in interval notation.
First, I'll isolate the quadratic on one side of the inequality, so I'll have zero on the other side:
x2 − 6x + 7 < 0
Now I want to find the zeroes. There are no factors of +7 that add to −6, so this quadratic doesn't factor. Instead, I'll use the Quadratic Formula:
![x = [−(−6) ± sqrt{(−6)^2 − 4(1)(7)}] / [2(1)] = [6 ± sqrt{36 − 28}] / [2] = ... = 3 ± sqrt{2}](ineqsolv/quad16a.png)
The "minus" zero is smaller than the "plus" zero; the approximate decimal values of these zeroes (if you were graphing this) are 1.58579 and 4.41421.
This is a positive quadratic, so it's an upward-opening parabola. I'm needing to find the interval(s) over which the quadratic is negative.
But I don't need a graph to find the solution interval(s); I know that this quadratic's upward-opening parabola can be below the x-axis only in the middle of the graph, between the two x-intercepts. So my answer, in interval notation, is:
Much ("most"?) of the time, the quadratics they give you in these inequalities will be factorable. But, for any quadratic that is not factorable (and for ones where you just don't feel like factoring), you can always use the Quadratic Formula. It's perfectly okay for solution values and interval endpoints to be messy. "Messy" does not necessarily mean "wrong".
© 2024 Purplemath, Inc. All right reserved. Web Design by 