Exponential Functions: Introduction

How do you know if a function is exponential?

If the function's rule can be expressed as ab^x, then the function is exponential. If the graph shows that the height doubles over regular intervals (like every 5 units), then the function is exponential.

What are the properties of an exponential function?

An exponential function has the following characteristics:

• The graph has a y-intercept.
• The graph has a horizontal asymptote on the portion of the graph where the power is negative.
• The domain is all real numbers; there is no limitation on the value of x.
• The function has a constant growth factor and a fixed doubling period.

How do you write an exponential function?

In general, an exponential function is written as f (x) = a b^x or as f (x) = a b^cx, where a, b, and c are constants.

---

Previously, you have dealt with such functions as f (x) = x², where the variable x was the base and the number 2 was the power. In the case of exponentials, however, you will be dealing with functions such as g(x) = 2^x, where the base is the fixed number, and the power is the variable.

Let's look more closely at the function g(x) = 2^x. To evaluate this function, we operate as usual, picking values of x, plugging them in, and simplifying for the answers. But to evaluate 2^x, we need to remember how exponents work. In particular, we need to remember that negative exponents mean "put the base on the other side of the fraction line".

Zero and positive x-values give us y-values like these:

As you can see, for each increase of x by 1, the output y-value doubled. For this exponential, the doubling period is 1. This means that the values would continue to climb — 64, 128, 256, 512, 1024 — and quickly become unreasonably large for graphing.

Negative x-values return values like these:

Wow, those numbers are getting really small! And at every step, the values are getting cut in half. They're practically equal to zero, at least as far as graphing is concerned.

Some of the y-values were getting a little large for the graph, and some of the numbers were so small as to be kind of pointless (as far as graphing is concerned). So we won't necessarily try to plot every single point we've found. Putting together some "reasonable" (that is to say, nicely graphable) points, this is our T-chart:

...and this is our graph:

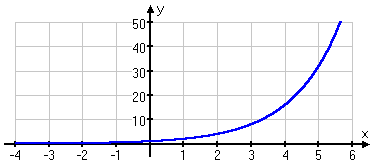
Just as the T-charts had suggested, the exponential started small (though positive), and eventually started zooming upward.

---

You should expect graphs of exponentials to have an arcing-upward form. That is, they'll start small — very small, so small that they're practically indistinguishable from "y = 0", which is the x-axis — and then, once they start growing, they'll grow faster and faster, so fast that they shoot right up through the top of your graph.

You should also expect that your T-chart will not have many useful plot points. For instance, for x = 6 or x = 10, the y-values would have been too big, and for just about all the negative x-values, the y-values will be too small to see, so you would just draw the line right along the top of the x-axis.

Special note: Take a close look at my graph above; my axis scales do not match. The scale on the x-axis is much wider than the scale on the y-axis; the scale on the y-axis is compressed, compared with that of the x-axis.

You will probably find this altered-scale technique to be useful when you're graphing exponentials, because of the way that the exponentials grow so quickly. You will find a few T-chart points, and then, with your knowledge of the general appearance of exponentials, you'll do your graph, with the left-hand portion of the graph usually running right along the x-axis. A compressed vertical axis allows you to show more without taking up the entire sheet of paper. But when you use scales that don't match, make sure that you label the scales very clearly.

---

What is "exponential growth"?

Exponential growth is growth which can be modelled with an exponential function. Exponential growth has the property of having a doubling period; for instance, a colony of bacteria in a petri dish might double in size every six hours. Exponential growth generally starts slow but, once it gets going, it grows very, very quickly.

The term "exponential growth" is often used informally in conversation, the news, etc, to stand for "really, really fast" growth, which may not actually have a doubling period. Keep this distinction in mind: in math, there is a precise definition; in common usage, the meaning is more fluid. So if you hear somebody claiming that the world population is doubling every thirty years, you know he is claiming exponential growth.

How does exponential growth compare to polynomial growth?

Exponential growth is bigger and faster than polynomial growth. This means that, no matter what the degree is on a given polynomial, a given exponential function will eventually be bigger than the polynomial. Even though the exponential function may start out really, really small, it will definitely eventually overtake the growth of the polynomial and then zoom on past, doubling all the time.

For instance, x¹⁰ seems much bigger than 10^x, and initially it is:

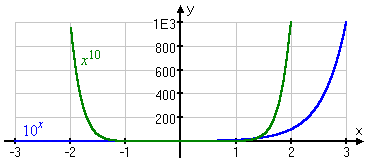
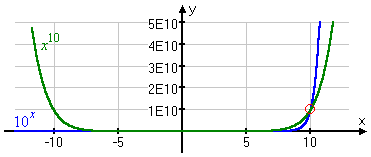
But eventually 10^x (in blue below) catches up and overtakes x¹⁰ (at the red circle below, where x is ten and y is ten billion), and it's bigger than x¹⁰ forever after:

---

Exponential functions always have some positive number — other than 1 — as the base. If you think about it, having a negative number (such as −2) as the base wouldn't be very useful, since the even powers would give you positive answers (such as "(−2)² = 4") and the odd powers would give you negative answers (such as "(−2)³ = −8"), and what would you even do with the powers that aren't whole numbers?

Also, having 0 or 1 as the base would be kind of dumb, since 0 and 1 to any power are just 0 and 1, respectively; what would be the point? This is why exponentials always have something positive and other than 1 as the base.