Ellipses: Finding Information from the Equation
Purplemath
Once you've been introduced to ellipses, one of your first tasks will usually be to demonstrate that you can extract information about an ellipse from its equation, and also to graph a few ellipses. These will involve some technical processes.
It will likely be wise to invest a little extra time and effort in practicing and memorizing the steps, so you're in good shape for the test.
- State the center, vertices, foci and eccentricity of the ellipse with general equation 16x2 + 25y2 = 400, and sketch the ellipse.
To be able to read any information from this equation, I'll need to rearrange it to get the variable terms grouped together, so I get an equation that is "=1". First, I'll divide through by the 400:
Since x2 = (x − 0)2 and y2 = (y − 0)2, the equation above can be more-helpfully restated as:
Then the center is at (h, k) = (0, 0).
I know that the a2 is always the larger denominator (and b2 is the smaller denominator), and this larger denominator is under the variable that parallels the longer direction of the ellipse. Since 25 is larger than 16, then a2 = 25, a = 5, and this ellipse is wider (paralleling the x-axis) than it is tall. The value of a also tells me that the vertices are five units to either side of the center, so they're at (−5, 0) and (5, 0).
To find the foci, I need to find the value of c. From the equation, I already have a2 and b2, so:
a2 − c2 = b2
25 − c2 = 16
9 = c2
Then the value of c is 3, and the foci are three units to either side of the center, at the points (−3, 0) and (3, 0).
Also, the value of the eccentricity e is .
To sketch the ellipse, I first draw the dots for the center and for the endpoints of each axis:
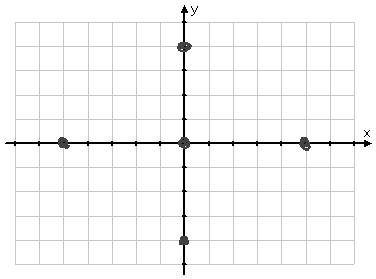
Then I rough in a curvy line, rotating my paper as I go and eye-balling my curve for smoothness...
...and then I draw my "answer" as a heavier solid line.
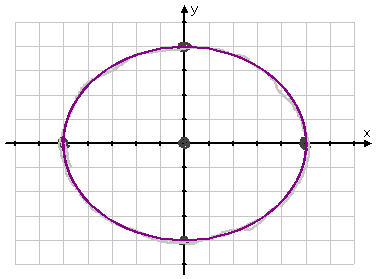
center: (0, 0)
vertices: (−5, 0) and (5, 0)
foci: (−3, 0) and (3, 0)
eccentricity:
You may find it helpful to do the roughing-in of your graph with pencil, rotating the paper as you go around, and then draw your final graph in pen, carefully erasing your rough draft before you hand in your work. And always make sure your graph is neat, that it is large enough to be clear, and that your curves are appropriately rounded. There are no straight, or even straight-ish, line segments on ellipses.
- State the center, foci, vertices, and co-vertices of the ellipse with equation 25x2 + 4y2 + 100x − 40y + 100 = 0. Also state the lengths of the two axes.
I first have to rearrange this equation into conics form by completing the square and dividing through to get "=1". Once I've done that, I can read off the information I need from the equation.
25x2 + 4y2 + 100x − 40y = −100
25x2 + 100x + 4y2 − 40y = −100
25(x2 + 4x ) + 4(y2 − 10y ) = −100 + 25( ) + 4( )
25(x2 + 4x + 4) + 4(y2 − 10y + 25) = −100 + 25( 4 ) + 4( 25 )
25(x + 2)2 + 4(y − 5)2 = −100 + 100 + 100 = 100
The larger demoninator is a2, and the y part of the equation has the larger denominator, so this ellipse will be taller than wide (to parallel the y-axis). Also, a2 = 25 and b2 = 4, so the equation b2 + c2 = a2 gives me 4 + c2 = 25, and c2 must equal 21.
The center is clearly at the point (h, k) = (−2, 5). The vertices are a = 5 units above and below the center, at (−2, 0) and (−2, 10). The co-vertices are b = 2 units to either side of the center, at (−4, 5) and (0, 5). The major axis has length 2a = 10, and the minor axis has length 2b = 4.
The foci are messy: they're units above and below the center.
center: (−2, 5)
vertices: (−2, 0) and (−2, 10)
co-vertices: (−4, 5) and (0, 5)
foci: ![(-2, 5 - sqrt[21])](conics/ellipse13.gif){kind=small}
and ![(-2, 5 + sqrt[21])](conics/ellipse14.gif){kind=small}
major axis length: 10
minor axis length: 4
As in the example above, you may be given the ellipse's equation in "general" form; that is, with everything multiplied out, so there are no denominators and no parentheticals. But to extract the information from the equation, you need the equation in conics form. To go from the general form to the conics form, you'll need to be sure that you can reliably complete the squares. If you're not comfortable with that process, give yourself some time to do some extra practice before the next test.
© 2024 Purplemath, Inc. All right reserved. Web Design by 