Completing the Square with Ellipses
Purplemath
How do you find the center/vertex form of an ellipse?
To convert an ellipse's equation from "general" form (that is, from fully-multiplied-out form) to center/vertex form (that is, the form where it's easy to find the center and vertices), you have to complete the square for the x- and y-containing terms.
Content Continues Below
Any loose numbers get collected on the other side of the "equals" sign, and then you divide through by the resulting number to get 1.
The multiplied-out form of the equation for an ellipse looks something like this:
Ax2 + By2 + Cx + Dy + E = 0
But the more useful form of the equation — the form from which you can easily find the center and the two sets of vertices of the ellipse — looks quite different:
...where the point (h, k) is the center of the ellipse, and the focal points and the axis lengths of the ellipse can be found from the values of a and b.
But how do you convert from the general form to the useful form? By completing the square.
Affiliate
Advertisement
What are the steps in completing the square for an ellipse?
The steps to completing the square for an ellipse are these:
- If necessary, move any strictly numerical term to the other side of the "equals" sign from the variable-containing terms.
- Collect the x-containing terms together, followed by the y-containing terms.
- Whatever is multiplied on the squared-variable terms, factor that out of that variable's terms.
- Divide through by whatever you factored out of the x-collection; then divide through by whatever you factored out of the y-collection. Expect to get fractions as a result.
- Complete each of the two squares by dividing the linear terms' coefficients by 2 and squaring; add the same squared number to the other side of the "equals" sign, remembering to include whatever is multiplied on that variable's grouping.
- Simplify the numerical stuff on the other side of the "equals" sign.
- If the numerical stuff has a value other than 1, divide through by this value, so you have 1 opposite the variable stuff.
- Simplify the variable side.
Here's what that looks like:
- Find the focus equation of the ellipse given by 4x2 + 9y2 − 48x + 72y + 144 = 0.
To find the focus form of the equation, I must complete the square. To accomplish this, I follow the following procedure:
This is my original equation.
4x2 + 9y2 − 48x + 72y + 144 = 0
My first step is to move the loose number over to the other side of the "equals" sign, and group the x-stuff and y-stuff together.
4x2 − 48x + 9y2 + 72y = −144
Then I factor out whatever is multiplied on the squared terms.
4(x2 − 12x) + 9(y2 + 8y) = −144
I divide through by whatever I factored out of the x-stuff.
And I divide through by whatever I'd factored out of the y-stuff.
Content Continues Below
To prepare to complete the squares, I leave space in the x-stuff, the y-stuff, and on the right-hand side of the equation. Whatever numbers are multiplied on each of the x-stuff and the y-stuff, I multiply them onto the (empty) spaces on the right-hand side.
I then take half of the coefficients of the first-degree (that is, the linear) variable terms (being careful not to forget their signs!), square them, and add the squares into the appropriate spaces on both sides of the equation. I'll show the x and y parts separately:
For the x terms, the coefficient of the linear term is −12. Half of this is −6. The square is 36. So I insert 36 into each of the two x parentheticals:
For the y terms, the coefficient of the linear term is +8. Half of this is +4. The square is 16. So I insert 16 into each of the two y parentheticals:
Putting it all together, the spacing, halving, and squaring steps look like this:
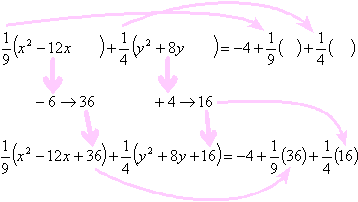
I simplify the strictly numerical stuff on the right-hand side.
To convert the completed squares in the left-hand side to squared form (that is, to convert the perfect-square trinomials into squared-binomial form), I use the values I got when I divided the linear coefficients by 2. (This is where I use those signs I kept track of earlier.)
To finish up, I divide through by the numerical value on the right-hand side of the "equals" sign, so the right side becomes "=1":
Affiliate
By the way, the process for hyperbolas is the same, except that the signs on the x-squared and y-squared terms will be opposite; that is, while both the x-squared and y-squared terms are added in the case of ellipses (and circles), one or the other will be subtracted in the case of hyperbolas.
URL: https://www.purplemath.com/modules/sqrellps.htm
You can use the Mathway widget below to practice completing the square for ellipses. Try the entered exercise, or type in your own exercise. Then click the button and select "Write in Standard Form" to compare your answer to Mathway's.
Please accept "preferences" cookies in order to enable this widget.
(Click "Tap to view steps" to be taken directly to the Mathway site for a paid upgrade.)
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()




