Does the Bible really say that π = 3?
Do the Nevi'im and the Ketuvim (sections of Jewish scripture, comprising parts of the Christian "Old Testament") really say that the value of π is three? Not actually, but I keep receiving queries on this issue. (Note: I practice neither Judaism, Christianity, nor Islam. I have no dog in this fight. I'm just answering the question.)
Before we do the calculations to put this old chestnut to rest, let's lay a little groundwork.
What is the text that they use?
People use the following portion of the text as the basis of their claim:
"And he [Hiram] made a molten sea, ten cubits from the one rim to the other it was round all about, and...a line of thirty cubits did compass it round about....And it was an hand breadth thick...." — First Kings, chapter 7, verses 23 and 26
There is a similar description in Second Chronicles 4, verses 2 through 5.
Who was Hiram?
Hiram was a Phoenician (foh-NEE-shun) artisan. The Phoenicians lived in what is now Lebanon. They were the creators of "royal purple", which was made by boiling a particular sea snail. (The process stank to high heaven; you could smell when you were getting close.) While the Phoenicians did not invent glass, they did invent glass-blowing. They invented the first alphabet, from which we derive our own Latin alphabet. And they were skilled builders and artisans who exported their talents along with their legendary wood products, the fabled "cedars of Lebanon".
Hiram was the Phoenician artisan recorded as having been hired by King Solomon (of Israel) to design and supervise the building of the Jewish temple. The huge bowl (or "sea") at issue was used within the temple for ceremonial washing.
What are the measurements in question?
The text refers to dimensions measured in cubits and handbreadths.
Back in those days, measurements were not standardized as they are now. People used seat-of-the-pants measurements. Have you ever estimated the width of a bookcase by seeing how long it was compared to your outstretched arms? And then walked over to the spot where you wanted to move the bookcase, and stood against the wall, making sure that the length you'd just measured against your own body would fit in the open space? If so, then you have used measurements similar to those that ancient civilizations used.
Advertisement
What is a cubit?
A cubit was the length from the elbow to the tip of the outstretched fingers. It is commonly standardized today as being about eighteen inches (or about forty-six centimeters). To measure the length of a desk, say, in cubits, you would put your elbow at one end of the desk, with your hand outstretched toward the other end of the desk. Put the index finger of your other hand on the desk where your outstretched fingertips end, to mark the end of that cubit. Then move your cubit-arm over your index finger (which is marking the first cubit) so your elbow is now at your index finger, with your outstretched fingers still aiming at the other end of the desk. This measures two cubits. Continue laying out cubits until you run out of desk, counting as you go. My desk, being seventy-two inches long, comes out to being about four and a half cubits long, as measured by my forearm.
What is a handsbreadth?
A handsbreadth is the "hand" used to measure horses. That is, it is the width of the palm of the person doing the measuring, and is standardized as being four inches (or about ten centimeters). To measure the height of the desk, start at the floor. Open your left hand with your palm facing toward you and your thumb up in the air (so it's out of the way). Rest your hand on the floor, with the back of your open hand against the desk, your palm still facing you, and your pinkie finger on the floor. Now open your right hand (again sticking your thumb up in the air so it's out of the way), and rest it on top of your left hand (so your right pinkie finger is across the top of your left index finger). This measures two hands. Continue alternating hands up the side of your desk, counting as you go. My desk, being thirty inches tall, comes out to being about eleven handbreadths, as measured by my skinny little hands.
Since cubits and handbreadths are measured against a person's body, and since bodies vary, actual measurements (as opposed to standardized measurements) will vary from person to person. Your desk might be thirty inches tall, just like mine, but you might have bigger hands, so you might get a body-measure of only ten handbreadths. This variation is normal.
Since we have no idea what Hiram's body measurements were, we'll have to approximate by using the standardized values for cubits and handbreadths.
What are some reasonable assumptions?
If this discussion of a "sea", or large bowl, had been referring to what is called an "ideal" bowl (that is, to a mathematical object, not existing in a physical sense, and having no thickness that could be felt or handled), then the text would indeed be claiming that the value of π is three. But we can safely assume that the text is referring to a real-world physical object, having the thick sidewalls necessary to support its own weight.
Now that you know how to measure cubits, can you see that it would be rather difficult to measure the curved surface of a bowl in cubits? Instead, we can assume that a straightened rope would be used to measure the length. The rope would then have been moved to outline a circle with the desired circumference. Also, Hiram would not have just tossed some brass in the furnace and waited to see what came out. We can assume that he would have designed the piece and would have given his workmen instructions.
It seems reasonable to assume that making a "sea" like this would have required a mold. The outer mold would have one dimension, and the inner mold would have another. And Hiram would have given his workmen instructions regarding these measurements.
Wouldn't it be reasonable to assume that the Phoenicians, being the renowned craftsmen that they were, had discovered a "rule of thumb"? Perhaps something along the lines of, "If a bowl is made with a three-to-one ratio between the inner circumference and the outer diameter, the bowl will have a desirable wall thickness that will support its own weight"? When Egyptians and Babylonians came up with rules of thumb or accidentally discovered formulae like this, we credit them with being clever. Can't we do the same for the Phoenicians, even if they did occasionally — gasp! — cooperate with Jews?
Now that you have some background information, let's look at the actual numbers.
Content Continues Below
What are the calculations?
Here again is the quote being referred to:
"And he [Hiram] made a molten sea, ten cubits from the one rim to the other it was round all about, and...a line of thirty cubits did compass it round about....And it was an hand breadth thick...." — First Kings, chapter 7, verses 23 and 26
The bowl is said to have had a circumference of thirty cubits and a diameter of ten cubits. The diameter is said to be "from one rim to the other", so this would be the outer diameter; that is, the diameter of the outer mold used to make the bowl.

The circumference is not specified as being the inner or outer circumference, but since using the outer circumference would give us the "ideal" bowl (that is, a bowl having no width or thickness), let's instead use the inner circumference, which also, reasonably, would have been the circumference of the mold used to form the inside of the bowl. That is, we will use the two measurements which were necessary for the casting of the piece.
Using eighteen inches for one cubit, we have the following:
outer diameter: 10 cubits, or 180 inches
outer radius: 5 cubits, or 90 inches
inner circumference: 30 cubits, or 540 inches
To find the "Jewish" or "Bible" value for π, we need to have the inner radius. Once we have that value, we can plug it into the formula for the circumference and compare with the given circumference value of 540 inches.
Since the thickness of the bowl is given as one handsbreadth, then the inner radius must be:
90 − 4 = 86 inches
Let's do the calculations:
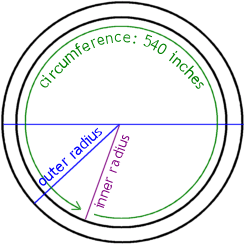
inner radius: 86 inches
inner circumference: 540 inches
The circumference formula is C = 2πr, which gives us:
540 = 2π(86)
540 = 172π
Solving, we get:
...or about 3.14.
Um... Isn't "3.14" the approximation we all use for π? Perhaps those Phoenicians were fairly accurate after all.
URL: https://www.purplemath.com/modules/bibleval.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()


