Explanation(s) for Dividing by a Fraction

What is "flip and multiply"?

"Flip and multiply" is the rule for dividing by a fraction. It means that, to divide by a fraction, you follow these steps:

1. Take the fraction that you're dividing by (that is, the fraction that is after the division symbol). (If the division is written as a stacked fraction, you'll be taking the fraction that is underneath.)
2. Make the reciprocal of that fraction (that is, flip the fraction over so, say, becomes ).
3. Bring the reciprocal up, next to whatever it was being divided into.
4. Replace the "divided by" with "multiplied by".
5. Do the multiplication in the usual way.

In other words, rewrite the division by keeping the top number the same, changing the division into multiplication, and then multiply that top number by the flip of the fraction. This is sometimes denoted as kcf, for "Keep, Change, Flip".

What is a rhyme for flip-n-multiply?

Various short poems have been written to help people remember how to divide by a fraction. You can search online for loads of them. Yes, many of them are a bit painful to read. (Stick to one meter, folks!) One of the less painful options is:

What is a song for flip-n-multiply?

There are also some videos with songs to help you remember the flip-n-multiply rule (that is, the Keep, Change, Flip rule) for dividing fractions, such as:

Whatever the mnemonic (like KCF), the shorthand (like flip-n-multiply), the poem, or the song, the method is always the same: Take the divided-by fraction, flip it over, and make it a multiplied-by fraction.

What are the rules for flip-n-multiply?

The "rules" for flip-n-multiply (or Keep, Change, Flip, and then multiply) are contained in the names for the process: You keep the number that was being divided by the fraction the same, you flip the divided-by fraction, change the divided-by into multiplied-by, and then multiply (and simplify, if needed).

Which side do you flip?

When you flip-n-multiply, you always flip the fraction after the division symbol. (Or, if the division is written as a stacked fraction, then you flip the fraction that's underneath.) For instance:

...or, as a stacked fraction:

Do you always flip-n-multiply when dividing by a fraction?

There are other ways of dealing with a divided-by fraction, but they're all more painful than Keep, Change, Flip, and multiply. So, in practical terms, yes, you'll always want to flip-n-multiply when dividing by a fraction.

---

Why flip-n-multiply? Why does Keep, Change, Flip work?

The most basic reason that flip-n-multiply works is that division can be defined as "multiplying by the reciprocal". We define division as being the corresponding equality to a multiplication. For instance, we say that 8 ÷ ½ = 16 because 8 × 2 = 16. (The whole number 2, as a fraction, is , which is the reciprocal of ½.)

Note that subtraction of a number can be defined as the addition of the negative of that number. That is, subtraction can be defined as:

Just as subtraction can be defined as the addition of the additive inverse, so also division can be defined as the multiplication of the multiplicative inverse (that is, multiplication by the reciprocal, giving you 1).

While mathematics does run on definitions, this "explanation" may feel a bit like a cheat. But:

Flip-n-multiply can also be justified by formatting the division as a stacked fraction, and simplifying by getting rid of the denominator. Remember that any number (other than zero), when multiplied by its reciprocal, gives you 1. So we multiply, top and bottom, by the reciprocal of the current denominator, because this will make the denominator go away:

The fraction five-thirds, when divided by itself, turns into 1, so multiplying the original division, top and bottom, by five-thirds is the exact same thing as multiplying by 1. The value of the original expression remained unchanged — but the formatting changed, and in a useful direction.

Multiplying the three-fifths underneath (that is, multiplying the original divided-by) by the five-thirds collapsed the denominator into a simple 1. And the numerator was thereby changed to multiplying by the reciprocal.

(This is one of the other methods for dividing by a fraction. As you can see, it ends up being nothing more than flipping and multiplying. But it's a lot more steps, so why bother, right?)

Related to this, we can justify flip-n-multiply by converting the fractions to a common denominator. For instance, using the previous division:

...we can convert the whole number to fractional form with a deniminator of 75:

So, whatever we have (and we have a bunch of fifths), we're taking 75 of them and dividing them into three groups. How many must then be in each group? Twenty-five, which is the same answer we got before.

We can also think of division as splitting something into certain-sized pieces. If I bring a twelve-pack to your barbeque, how many people can have two of my sodas? We divide 12 by 2 and get 6. So far, so good.

Now let's suppose that I've brought my twelve-pack to the neighbor kid's sixth birthday, and the sodas will be poured into individual cups, one-third of a can each. Into how many one-third-cans can the twelve-pack be split?

Each can will be split into three one-thirds. With twelve cans, this gives us 36 cups of soda for the little kiddos. In other words:

In the above case, flip-n-multiply gave us the same result that we already intuitively expected. Let's get a bit more complicated:

Suppose now that you had a pizza party and, after everyone's gone home, you find that you have one and a half pizzas left over; that is, you have three-halves of a pizza left. You figure you'll eat half of a pizza for your lunch. How many one-half-pizza lunches can you have?

You probably almost instantly knew the answer. You've got three-halves, and you're going to have a half for lunch. You can split the three-halves into three halfs, so you have have half of a pizza for your next three lunches. Mathematically, we're dividing by , and getting 3:

Let's make the situation a bit more complicated. You've got the one and a half pizza left over, but now let's say that you want to have one-third of a pizza for lunch. How many one-third-pizzas can you get from three-halves pizzas?

Halves and thirds don't play well together, but each can be converted into sixths. So each half can be cut into three pieces. With three halves, we end up with nine pieces that are each one-sixth of a pizza, or nine-sixths of a pizza in total, like so:

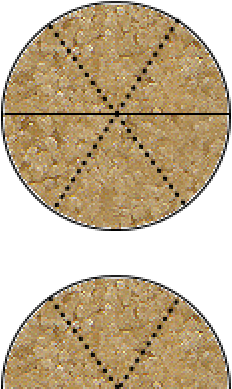
Remember that we're trying to figure out how many one-thirds we can divide out from the current one and a half pizzas. So we are doing this:

...or, in numerical terms:

Just noodling this around in our heads (and peeking back at the pictures), we can see that the one (whole) pizza will be split into three one-third-pizza pieces. From the other half-pizza (which is now three-sixths of a pizza), we can take another one-third-pizza serving (which is two-sixths of that remaining half-pizza). But that will leave a one-sixths piece left over. And one-sixth is half of one-third (as you can see in the picture). We're talking in terms of one-third-pizza servings, so the leftover one-sixth would be half of a serving.

In other words, when we go to split the remaining pizza into one-third-pizza servings, we know that we will get four one-third servings, with half of a serving left over. Mathematically, we can already see the answer:

Now let's convert the mixed number to improper-fraction form, and flip-n-multiply. Does Keep, Change, Flip match what we already know from practical experience?

And, of course, nine half-servings is four whole servings, with half of a serving left over. The math matches what we already knew. Flip-n-multiply is something we've been doing all along, but without realizing it. Keep, Change, Flip works. It makes sense, because it matches real life.