The Unit Circle: More Examples
Purplemath
When working with the unit circle, it can be helpful to make sketches. Don't try to rely only on your memory. Use whatever tools you find helpful.
In what follows, I'll show my "scratch-work" as part of my solution process. Note that not all instructors like to see pictures. I even had one instructor who said that he'd take points off of any question that had a picture drawn. I still drew the pictures; I just made very sure that I'd erased them cleanly before handing in the test. But at least when you're just getting started, re-working examples from the book or your class notes, draw any pictures that you find useful!
-
Find the value of sec(225°) and tan(225°).
The angle measure is between 180° and 270°, so I know that this angle ends in the third quadrant. So I'll draw my unit circle with an ending angle side in QIII:
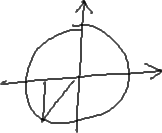
(Yes, my drawing is messy. It doesn't matter. I'm just using it as a placeholder for the values I need to track. There's no need for a compass or ruler in this scratch-work.)
To see if the given angle is related to one of the basic reference angles whose values I've memorized, I'll subtract the given angle from the angle measure at the upper end of QIII, being 270°:
270 − 225 = 45
Okay, so this is the basic 45-45-90 triangle, whose legs (in the unit circle) have lengths of . The hypotenuse is, as always in the unit circle, equal to 1. I'll label the corresponding triangle in the first quadrant:
![unit circle, with 45-45-90 triangle drawn in first quadrant; legs are labelled as "1/sqrt[2]", and hypotenuse is labelled as "1"](trig/unitci08.gif)
In the third quadrant, the x- and y-values are negative. I'll label the legs of the triangle in QIII:
Now I can read the trig ratios from the picture. I know that secant is the reciprocal of cosine; cosine is "adjacent over hypotenuse", so:
The tangent is "opposite over adjacent", which gives me:
I know that tangent is positive in QIII, while cosine is negative, so I can see that the signs on my values are correct (and doing this sign-check gives me a useful confirmation that I'm probably doing this right). My final answer is:
tan(225°) = 1
Take another look at the circle I drew above, with two angles shown. This can be extended to the other two quadrants, as well. If you're not sure how to draw your hypotenuse for a given angle, use the "bowtie" image:
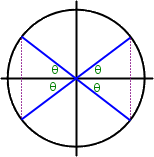
In the image above, the portion outlined by the blue terminal-angle sides and the dashed purple verticals mark off a shape that's reminiscent of a bowtie. These are the lines you'll want to draw.
-
Using the unit circle, find the value of the cosine of an unspecified angle α, given that .
Upon first reading this exercise, I'm wondering how the cosine of the unknown angle and the value of y could possibly relate. They haven't given me an angle measure or even a quadrant, and yet they want a trig-ratio value when all they've given me is half of an (x, y) point.
But then I remember that, on the unit circle, the sine of an angle is given by the y-value of the point at which the terminal side of the angle (that is, by the y-value of the point where the hypotenuse of the underlying triangle) crosses the unit circle. So they have actually given me enough to get started.
First, I'll draw my unit circle and dash in a line to indicate "":
Immediately, I notice that I can draw two triangles having this y-value, one in each of the third and fourth quadrants:
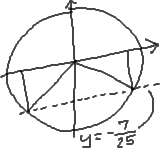
Because I'm using the unit circle, I know that the hypotenuse of each triangle has a length of 1, and they've given me the y-value. Putting this together with the Pythagorean identity, I get:
I got two values, a plus and a minus. Which is the correct one? Both are correct, matching the two triangles that I had in my drawing. So my answer is:
Another potential use of the unit circle is a means of reminding yourself of where tangent, cotangent, secant, and cosecant are undefined. Since you can state the values of the trig ratios in terms of x and y, and since you can see (on the circle) where x (for the tangent and secant) and y (for the cotangent and cosecant) are zero (being the axes). Since we can't divide by zero, then these trig ratios are undefined at these points.
The unit circle is just another tool for keeping track of trig ratios, finding and "seeing" relationships, and solving exercises. Don't overthink it. Just use it whenever and wherever you find it to be helpful.
© 2024 Purplemath, Inc. All right reserved. Web Design by 