Finding Trig Ratios for Larger Angles
Purplemath
On the previous page, we saw how we could expand the context of the trigonometric ratios from the geometric one of right triangles to the algebraic one of angles being based at the origin and using angles of any measure.
This disconnects the trig ratios from physical constraints, allowing the ratios to become useful in many other areas of study, like physics and engineering.
To refresh:
How do you find trig ratios for angles more than ninety degrees?
To find the values of trigonometric ratios when the angles are greater than 90°, follow these steps:
- In the x,y-plane, draw the terminal side of the angle.
- Draw a line from this terminal line to the x-axis, perpendicular to the x-axis.
- Within the right triangle formed by the axis, the terminus line, and the perpendicular, label the base angle (at the origin) with its size within that quadrant of the plane. For instance, an angle of 120° becomes a triangle in the second quadrant, with a base-angle measure of 180° − 120° = 60°.
- Label the axis length and the perpendicular with their values in that quadrant. For instance, for the 60° angle in the second quadrant, the "opposite" value (being the height y) is positive, but the "adjacent" side (along the x-axis) is negative.
- Use the Pythagorean Theorem to find the value of the hypotenuse, if needed. (This value will always be positive.)
- Once all three sides are labelled, with their signs, read off the ratios directly from the picture.
With just a little practice, the above process should become pretty easy to do. Let's look at an example.
- Find the six trigonometric ratios for the angle having point (4, −3) on its terminal side.
First, I'll draw a picture showing the two axes, the given point, the line from the origin through the point (representing the terminal side of the angle), and the angle θ formed by the positive x-axis and the terminus:
Yes, this drawing is a bit sloppy. But my picture doesn't need to be exact or "to scale". It's just a placeholder. I only need the general idea of what quadrant I'm in and where the angle θ is.
Now that I've drawn the angle in the fourth quadrant, I'll drop the perpendicular down from the axis down to the terminus:
This gives me a right triangle in the fourth quadrant. I can work with this.
From the x- and y-values of the point they gave me, I can label the two legs of my right triangle:
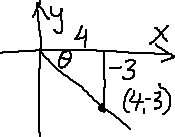
Then the Pythagorean Theorem gives me the length r of the hypotenuse:
r2 = 42 + (−3)2
r2 = 16 + 9 = 25
r = 5
Now I'll finish my picture by adding the length of the hypotenuse to my right triangle:
And this gives me all that I need for finding my ratios. To find my answers, I can just read the numbers from my picture:
Sometimes you'll be given some fragmentary information, from which you are asked to figure out the quadrant for the context.
- Determine the quadrant in which lies the terminal side of the angle θ, given that tan(θ) < 0 and sin(θ) < 0.
For this exercise, I need to consider the x- and y-values in the various quadrants, in the context of the trig ratios. I don't need to find any actual values; I only need to work with the signs and with what I know about the ratios and the quadrants.
The tangent ratio is y/x, so the tangent will be negative when x and y have opposite signs. This occurs in the second quadrant (where x is negative but y is positive) and in the fourth quadrant (where x is positive but y is negative). So the sign on the tangent tells me that the end of the angle is in QII or in QIV.
The sine ratio is y/r, and the hypotenuse r is always positive. So the sine will be negative when y is negative, which happens in the third and fourth quadrants.
So the tangent is negative in QII and QIV, and the sine is negative in QIII and QIV. The overlap between the two solutions is QIV, so:
terminal side of θ: QIV
The thought process for the exercise above leads to a rule for remembering the signs on the trig ratios in each of the quadrants.
What are the signs of sine, cosine, and tangent in the four quadrants?
Using the signs of x and y in each of the four quadrants, and using the fact that the hypotenuse r is always positive, we find the following:
- In the first quadrant, all the values (x, y, and r) are positive, so All the trig ratios are positive.
- In the second quadrant, the x-values are negative, so x/r and y/x are negative; only y/r is positive, so only the Sine is positive in QII.
- In the third quadrant, each of x and y is negative, so x/r and y/r are negative; only y/x is positive, so only the Tangent is positive in QIII.
- In the fourth quadrant, the y-values are negative, so y/r and y/x are negative; only x/r is positive, so only the Cosine is positive in QIV.
You're probably wondering why I capitalized the trig ratios and the word "All" in the preceding paragraph. I did that to explain this picture:
The letters in the quadrants stand for the initials of the trig ratios which are positive in that quadrant.
What mnemonics can help you remember where each of sine, cosine, and tangent is positive?
Some people remember the letters indicating positivity by using the word "ACTS", but that's the reverse of normal (anti-clockwise) trigonometric order. Others remember the letters with the word "CAST", which is the normal rotational order but doesn't start in the usual (first-quadrant) starting place.
To start in the usual spot and rotate in the usual direction, still others use the mnemonic "All Students Take Calculus" (which is so not true). Use whichever method works best for you.
- Find the values of the remaining trigometric ratios, given that and θ lies in QIII.
From the sign on the cosine value, I only know that the angle is in QII or QIII. That's why they had to give me that additional specification: so I'd know which of those two quadrants I'm working in.
I'll start by drawing a picture of what I know so far; namely, that θ's terminal side is in QIII, that the "adjacent" side (along the x-axis) has a length of −8, and that the hypotenuse r has a length of 17:
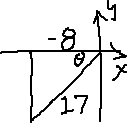
(For the length along the x-axis, I'm using the term "length" loosely, since length is not actually negative. Expect to hear "length" used this way a lot in this context.)
The Pythagorean Theorem gives me the length of the remaining side:
172 = (−8)2 + y2
289 = 64 + y2
225 = y2
±15 = y
Since I'm in QIII, I'm below the x-axis, so y is negative. Therefore, I'll take the negative solution to the equation, and I'll add this to my picture:
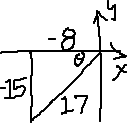
Now I can read off the values of the remaining five trig ratios from my picture:
© 2024 Purplemath, Inc. All right reserved. Web Design by 