Extracting a Parabola's Equation from its Info
Purplemath
How do you get a parabola's equation from its info?
If you are given some of a parabola's information, you can plug this information into one or another of the forms of the parabola's equation, and simplify. There will often be little more that you need to do.
For instance, if you are given the vertex (h, k) and the directrix x = a of a parabola, then you can plug this information into the vertex form of the parabola's equation, and that is your answer; nothing more is required.
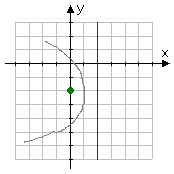
- Write an equation for the parabola with focus at (0, −2) and directrix x = 2.
The vertex is always halfway between the focus and the directrix, and the parabola always curves away from the directrix, so I'll do a quick graph showing the focus, the directrix, and a rough idea of where the parabola will go:
So the vertex, exactly between the focus and directrix, must be at (h, k) = (1, −2). (This sketch, by the way, while extrememly helpful to me, is just scratch-work; I should not hand this in as part of my homework solution.)
The absolute value of p is the distance between the vertex and the focus and also the distance between the vertex and the directrix. Since the focus and directrix are two units apart, then the size of p has to be one unit, so | p | = 1.
Since the focus is to the left of the vertex and directrix, then the parabola faces left (as I'd shown in my picture) and therefore I get a negative value for p: p = −1 (and, in case I need it, this means that a = −4). Since this is a sideway parabola, then the y part gets squared, rather than the x part.
The conics form of the parabola's equation is:
4p(x − h) = (y − k)2
I'll plug my values into this equation:
4(−1)(x − 1) = (y − (−2))2
−4(x − 1) = (y + 2)2
Checking the original exercise statement, I see that they only asked me for "an" equation of the parabola; in particular, they did not specify which form of the equation I had to given them for my answer. If they'd asked for the general form, I'd have had to multiply things out, to get x = (−¼)y2 − y. But they didn't specify, so my hand-in answer is:
−4(x − 1) = (y + 2)2
- Write an equation of the parabola with vertex (3, 1) and focus (3, 5).
Since the x-coordinates of the vertex and focus are the same, then I know that they must be one of top of the other, so this is a regular vertical parabola, where the x part is squared.
Since the vertex is below the focus, this is a right-side up parabola, so p must be positive.
Since the vertex and focus are 5 − 1 = 4 units apart, then p = 4.
And that's all I need for my equation, since they already gave me the vertex.
(x − h)2 = 4p(y − k)
(x − 3)2 = 4(4)(y − 1)
(x − 3)2 = 16(y − 1)
- Write an equation for the parabola with vertex (5, −2) and directrix y = −5.
The directrix is an horizontal line. Since the directrix is perpendicular to the axis of symmetry, then I know that the axis of symmetry must be vertical, and therefore this must be a regular parabola, where the x part is squared.
The distance between the vertex and the directrix is:
|−5 − (−2)| = |−5 + 2| = 3
This tells me that the value of p must be 3.
Since the directrix is below the vertex, then this is a right-side up parabola, so p is positive: p = 3. And that's all I need to find my equation:
(x − h)2 = 4p(y − k)
(x − 5)2 = 4(3)(y − (−2))
(x − 5)2 = 12(y + 2)
© 2024 Purplemath, Inc. All right reserved. Web Design by 