The Change-of-Base Formula
Purplemath
I've listed many logs rules, and so far we've used all but the Change-of-Base Formula. (Okay, we haven't used the Base-Switch Rule, but I don't know where that would be useful anyway, and Base-Switch is just a special case of the Change-of-Base Formula, so I'm ignoring Base-Switch.)
Content Continues Below
You may have noticed that your calculator only has keys for figuring the values for the common (that is, the base-10) log and the natural (that is, the base-e) log. There are no calculator keys for any other bases.
Advertisement
Some students try to get around this by attempting to evaluate something like "log3(6)" with the following keystrokes:
LOG 3 ( 6 ) ENTER
Of course, they then get the wrong answer, because the above actually (usually) calculates the value of "log10(3) × 6". This is not what had been intended.
In order to evaluate a log with a non-standard base, you have to use the Change-of-Base Formula.
What is the Change of Base Formula?
The Change of Base Formula is a formula for converting a log expression from one base (usually one that you can't plug into your calculator) to a log-fraction expression with a different base (usually the common or natural base). Specifically, the Formula says the following:
Change-of-Base Formula:
Let b and d be two positive numbers, neither of which equals zero, and let x be any positive number. Then the following relationship holds:
What this rule says, in practical terms, is that you can evaluate a non-standard-base log by converting it to the fraction of the form "(standard-base log of the argument) divided by (same-standard-base log of the non-standard-base)". I keep this straight by looking at the position of things. In the original log, the argument is "above" the base (since the base is subscripted), so I leave things that way when I split them up:
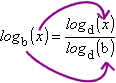
How does changing the log's base work (proof)?
To prove that the Change of Base Formula works, start by naming things. Let the original log base be b, and the new base be d; let the argument (that is, the insides) of the original log be x. Then the original log expression and the two log expressions in the log fraction that the Formula produces are (with names that I've given them) these:
logb(x) = r
logd(x) = s
logd(b) = t
The Relationship between logs and exponentials gives is the following equations:
(i) br = x
(ii) ds = x
(iii) dt = b
The equations (i) and (ii) tell us that (iv) br = ds. Equations (i) and (iii) tell us that (v) drt = br. Then equations (iv) and (v) tell us that ds = drt.
By nature of exponentiation, this means that s = rt. Plugging back in from the naming definitions at the beginning, this gives us:
s = rt
logd(x) = logb(x) × logd(b)
This proves the Change-of-Base Formula.
What does changing the base do to a log function?
When you use the Change of Base Formula to change the base of a log function, all that is changed is the form of the function. Instead of being one logarithm with a given base, the function becomes a fraction formed by two logarithms with whatever is the new base. All of the functional values remain the same; it is only the function's appearance (and the ability to evaluate that function in your calculator) that is changed.
Here's a simple example of this formula's application:
- Evaluate log3(6). Round your answer to three decimal places.
The argument is 6 and the base is 3. I'll plug them into the change-of-base formula, using the natural log as my new-base log:
Then the answer, rounded to three decimal places, is:
log3(6) = 1.631
Affiliate
I would have gotten the same final answer if I had used the common log instead of the natural log, though the numerator and denominator of the intermediate fraction would have been different from what I displayed above:
As you can see, it doesn't matter which standard-base log you use, as long as you use the same base for both the numerator and the denominator.
You can see in the above that the numerator of the base-10 common log did not match the numerator of the base-e natural log, nor did their denominators match. While I showed the numerator and denominator values in the above calculations, it is actually better to do the calculations entirely within your calculator, all in one go.
In other words, you don't need to bother with writing out that intermediate step showing the numerator and denominator values. Doing the whole thing in your calculator is your best bet for minimizing round-off errors.
In the above computation, rather than writing down the first eight or so decimal places in the values of ln(6) and ln(3) and then dividing, you would just do "ln(6) ÷ ln(3)" in your calculator.
Content Continues Below
You may get some simple (but fairly useless) exercises on this topic. Don't begrudge them; they're easy points, as long as you keep the change-of-base formula straight in your head. For instance:
- Convert log3(6) to an expression with logs having a base of 5
I can't think of any particular reason why a base-5 log might be useful, so I think the only point of these problems is to give you practice using change-of-base. Fine; I'll do the plug-n-chug:
They didn't ask me to evaluate anything; I didn't have to plug anything into a calculator or derive any numerical values. All this asked of me was that I do the conversion to a different base. So that one step of "work" is all that was required. It's really just that easy.
-
Convert ln(4) to an expression written in terms of the common log.
Why on earth would I want to do this (in "real life"), since I can already evaluate the natural log in my calculator? I wouldn't; this exercise is just for practice (and, on a test, it's easy points).
I'll plug-n-chug into the change-of-base formula:
Since getting an actual decimal value is not the point in exercises of this sort (the converting using change-of-base is the point), just leave the answer as a logarithmic fraction.
Affiliate
While the above exercises were fairly pointless, using the change-of-base formula can be very handy for finding plot-points when graphing non-standard logs, especially when you are supposed to be using a graphing calculator.
-
Use your graphing utility to graph y = log2(x).
If I were working by hand, I would use the definition of logs to note that:
- since 2-2 = ¼, then log2(¼) = -2
- since 2–1 = ½, then log2(½) = –1
- since 20 = 1, then log2(1) = 0
- since 21 = 2, then log2(2) = 1
- since 22 = 4, then log2(4) = 2
- since 23 = 8, then log2(8) = 3
- since 24 = 16, then log2(16) = 4
And then I would draw my graph by hand.
(Why did I pick these particular x-values? Because anything smaller would have been too tiny to graph by hand, and anything larger would have led to a ridiculously wide graph. I picked the values that fit my needs.)
But, in this case, I'm supposed to be doing the graph with my graphing calculator. How can I do this? (Or what if I'd just like to use my graphing calculator's "TABLE" feature to find some nice neat plot points?) I don't have a "log-base-two" button. However, I can enter the given function into my calculator by using the change-of-base formula to convert the original function to something that's stated in terms of a base that my calculator can understand. Flipping a coin, I choose the natural log:

(I could have used the common log, too. In that case, the function would have been "y1 = log(x)/log(2)".)
In my graphing calculator, after adjusting the viewing window to show useful parts of the plane, the graph will look something like this:

By the way, you can check that the graph contains the expected "neat" points (that is, the points I would have calculated by hand, as shown above) to verify that the picture displays the correct graph:
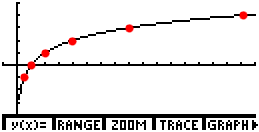
URL: https://www.purplemath.com/modules/logrules5.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()