Angles of Inclination / Declination
Purplemath
What is an angle of elevation / inclination?
An angle of elevation (also called an angle of inclination) is an angle that goes above the horizontal from whatever is the vantage point. For instance, suppose you are standing on the sidewalk looking up at the top of the chimney on the house across the street.
If there were a plank between where you're standing and that chimney's top, walking that plank would involve hiking up an incline. You must elevate your eyes (above the horizontal) to focus on that chimney. The angle above the horizontal that corresponds to your line of sight above the street between you and that house's chimney would be the angle of inclination (also called the angle of elevation).
What is an angle of depression / declination?
An angle of declination (also called the angle of depression) is an angle that goes below the horizontal from whatever is the vantage point. For instance, suppose you are standing on the balcony of your third-floor apartment and are wondering how far down the sidewalk is. The angle between the horizontal (being you looking across the parking lot to your friend on her third-floor deck in the next building over) and the sidewalk would be the angle of depression (also called the angle of declination).
What is the difference between angles of inclination/elevation and angles of declination/depression?
Angles of elevation/inclination are angles above the horizontal; angles of depression/declination are angles below the horizontal.
Whenever you have one of these angles, you should immediately start picturing how a right triangle will fit into the description.
- Driving along a straight flat stretch of Arizona highway, you spot a particularly tall saguaro ("suh-WAHR-oh") cactus right next to a mile marker. Watching your odometer, you pull over exactly two-tenths of a mile down the road. Retrieving your son's theodolite from the trunk, you measure the angle of elevation from your position to the top of the saguaro as 2.4°. Accurate to the nearest foot, how tall is the cactus?
Two-tenths of a mile is 0.2 × 5280 feet = 1056 feet, so this is my horizontal distance. I need to find the height h of the cactus. So I draw a right triangle and label everything I know:
The scale is not important; I'm not bothering to draw the angles or distances accurately. I'm just using the drawing as a placeholder — that is, as a way to keep track of information; the particular size is irrelevant.
What is relevant is that I have "opposite" and "adjacent" and an angle measure. This means I can create and solve an equation using the tangent ratio:
Checking the exercise statement, I am reminded that my unit is feet, and that I'm supposed to round. Then, to the nearest foot, the saguaro is:
44 feet tall
- You were flying a kite from the top of a bluff, but you managed somehow to dump your kite into the lake below. You know that you've given out 325 feet of string. A surveyor on his lunch break wanders over and tells you that the angle of declination from your position to the kite is 15°. How high is the bluff where you and the surveyor are standing? (Round your answer to the nearest whole number.)
First, I draw my triangle:
The horizontal line across the top is the line from which the angle of depression is measured. But by nature of parallel lines, the same angle is in the bottom triangle. I can see the trig ratios more easily in the bottom triangle, and the height is a bit more obvious. So I'll use this part of the drawing.
I have opposite, hypotenuse, and an angle, so I'll use the sine ratio to find the height.
Checking the exercise statement, I am reminded that my units are feet and that I'm supposed to round. Then the bluff stands above the lake at a height of:
about 84 ft
- A lighthouse stands on a hill 100 m above sea level, as shown in the graphic below. If ∠ACD measures 60° and ∠BCD is 30°, find the height of the lighthouse, to the nearest whole meter.
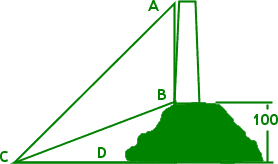
The first thing I notice is that, even without rounding, my answer can only be approximate, because lighthouses taper a bit as they go up. So the outer point of the lighthouse's base is not directly below the outer point of the top.
(But this is math, not real life, so it's okay to ignore this and just work from the picture they've given me.)
The second thing I notice is that I'm going to have to work this exercise in steps. I can't find the height of the tower, AB, until I have the length of the base CD. I will move the point D to the right, to meet the continuation downward of the height-line AB, forming a right triangle, as shown in my edited picture below:
Now I have two right triangles: triangle CAD and triangle CBD. I can work with this.
For my first computation to find the length of side CD, I'll use the height of the hill for the length of the opposite side of triangle CBD.
(To minimize round-off error, I'll use all the digits from my calculator in my computations, and try to carry the computations in my calculator the whole way.)
Now that I have the length of the base of triangle CBD (and thus for triangle CAD), I can find the total height of the hill-plus-lighthouse (that is, of the segment |AD|) by using the angle that measures the elevation from sea level to the top of the tower.
Excellent! By keeping all the digits and carrying the computations in my calculator, I got an exact answer. No rounding! But I do need to subtract, because "300" is the height from the water to the top of the tower. The first hundred meters of this total height is hill, so the tower is actually only:
200 meters tall
What are the steps for angles of inclincation/declination?
To sum up, the method for solving inclination/declination exercises is this:
- By definition, an angle of inclination or declination is measured with respect to some horizontal line. Draw that line, and the angle with respect to it.
- By definition, an angle of inclination or declination is relating that angle to the height (or depth) that an object is above (or below) the horizontal. Draw that height line. You should now have a right angle.
- The line-of-sight will be the hypotenuse of the right triangle. Draw this line.
- Solve the right triangle for the required information.
© 2024 Purplemath, Inc. All right reserved. Web Design by 