3-by-3 Determinants
Purplemath
The computations for evaluating 3×3 determinants are a bit lengthier than for evaluating 2×2 determinants, but the process I'll show you is fairly similar to what you use for 2×2's.
As before, we'll start with a square matrix (and, yes, the matrix must be square).
Content Continues Below
How do you do a 3×3 determinant (with examaple)?
We'll start with the following square 3×3 matrix A:
To create det(A), being the determinant for this matrix, we replace the square brackets with absolute-value bars:
Advertisement
The above is the determinant of the 3-by-3 matrix. As you can see, it contains the exact same entries as did the matrix, and in the exact same order.
But to find the value of that determinant (that is, to do our actual computations), we remove those bars (or at least we ignore the bar on the right-hand side) and extend the determinant's grid by rewriting the first two columns of numbers after (that is, to the right of) the third column in the grid of numbers. This gives us the following array:
Affiliate
When we were finding determinants of 2-by-2 matrices, we multiplied diagonally each way (up and down) and then subtracted the "up and to the right" value from the "down and to the right" value. With the extended grid of numbers that we've created here, we can do something similar.
Starting from the top left corner, we multiply along the (first three) down-diagonals:
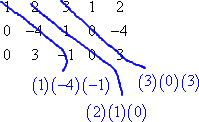
Then, starting from the bottom left corner, we multiply along the (first three) up-diagonals:
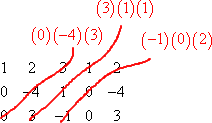
Add the down-diagonals and subtract the up-diagonals:
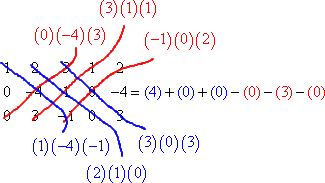
Note my use of parentheses above. This can help keep track of signs, especially if you're needing to subtract a negative number.
Now that I've done my multiplying, and have set up my additions and subtractions, it's time to simplify:
Then my hand-in answer is:
det( A ) = 1
Content Continues Below
What are the steps for evaluating a 3×3 determinant?
To evaluate (that is, to find the value of) the determinant of a 3-by-3 matrix, follow these steps:
- Remove the square brackets from the matrix
- Replace those brackets with absolute-value bars (this is the determinant)
- To do the computations, repeat the first two columns after the third column
- Multiply the values along each of the top-left to bottom-right diagonals
- Multiply the values along each of the bottom-left to top-right diagonals
- Add together the values found in step 4
- Add together the values found in step 5
- Subtract the value found in step 7 from the value in step 6, and simplify
- Find the deteriminant of the following matrix A:
First I convert from the matrix to the set-up for finding its determinant by removing the square brackets, and adding the first two columns to the right of the grid of numbers:
Then I multiply down and up the six diagonals:
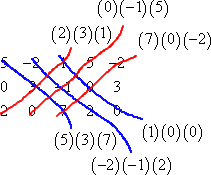
Finally, I add the down-diagonals, subtract the up-diagonals, and simplify for the final answer:
Then my hand-in answer is:
det( A ) = 103
Affiliate
There are other methods for simplifying determinants by hand, and these other methods are required when evaluating larger determinants by hand, but those methods can probably wait until later. If you're looking for a "quicker" or "easier" way to evaluate 3×3 determinants — well, there isn't one.
For the time being, note that your graphing calculator should be able to evaluate the determinant of any (square) matrix you enter. For instance:
![[C] = [[ 5 −2 1 ][ 0 3 −1 ][ 2 0 7 ]] then det([C]) = 103](matrices/determ20.gif)
But make sure, even if you have a graphing calculator, that you can evaluate 2×2 and 3×3 determinants by hand, because you are likely to be given word problems where the determinants contain variables that your calculator can't handle.
URL: https://www.purplemath.com/modules/determs2.htm
You can use the Mathway widget below to practice finding the values of 3-by-3 determinants. Try the entered exercise, or type in your own exercise. Then click the button and select "Find the determinant" to compare your answer to Mathway's.
Please accept "preferences" cookies in order to enable this widget.
(Click "Tap to view steps" to be taken directly to the Mathway site for a paid upgrade.)
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()




