Horizontal Asymptotes
Purplemath
What is a horizontal asymptote?
A horizontal asymptote for a rational function is a horizontal line, derived from the rational function, that shows you where the graph is, or thereabouts, when the graph goes off to the sides.
How does a horizontal asymptote differ from a vertical asymptote?
Vertical and horizontal asymptotes differ in the following ways:
- Whereas vertical asymptotes are sacred ground — which must never be touched — horizontal asymptotes are just useful suggestions.
- Whereas you can never touch a vertical asymptote, you can (and often do) touch and even cross horizontal asymptotes.
- Whereas vertical asymptotes indicate very specific behavior (on the graph), usually close to the origin, horizontal asymptotes indicate general behavior, usually far off to the sides of the graph.
- Whereas vertical asymptotes are found by locating the zeroes of the denominator, the horizontal asymptote is found by comparing degrees and perhaps doing some division.
Let's look at an example of finding horizontal asymptotes:
-
Find the horizontal asymptote of the following function:
![y = [x + 2] / [x^2 + 1]](rational/asympt09.gif){kind=small}
First, notice that the denominator is a sum of squares, so it doesn't factor and has no real zeroes. In other words, this rational function has no vertical asymptotes. So we're okay on that front.
As mentioned above, the horizontal asymptote of a function (assuming it has one) tells me roughly where the graph will being going when x gets really, really big, as it goes off to either side. So I'll look at some very big values for x; that is, at some values of x which are very far from the origin:
x |
![\\color{#404040}{y = [x + 2] / [x^2 + 1]}](rational/asympt10.gif){kind=small} |
−100 000 |
−0.0000099... |
−10 000 |
−0.0000999... |
−1 000 |
−0.0009979... |
−100 |
−0.0097990... |
−10 |
−0.0792079... |
−1 |
0.5 |
0 |
2 |
1 |
1.5 |
10 |
0.1188118... |
100 |
0.0101989... |
1 000 |
0.0010019... |
10 000 |
0.0001000... |
100 000 |
0.0000100... |
Off to the sides of the graph, where x is strongly negative (such as x = −1,000) or else strongly positive (such as x = 10,000) the +2 and the +1 in the expression for y really don't matter so much.
Why not? Because I ended up having a really big number divided by a really big number squared. The values of y came mostly from the x and the x2 parts, especially once x got very large. After all, a gazillion-plus-2 isn't that much difference from a gazillion.
The value of x2 is always going to be bigger than the value of just x, so the x2 value drags the value of the whole fraction down to something very close to y = 0 (that is, down to the x-axis) when x gets big.
This makes perfect sense, when you think about it. If you've got a gazillion (plus two, but who cares about that?) divided by a gazillion squared (plus 1, but who cares about that?), then you've essentially got a gazillion divided by the square of a gazillion, which simplifies to 1 over a gazillion. Which is going to be a very, very small number — practically zero, in fact. So of *course* the value of the function gets very, very small; of *course* it gets very, very close to zero.
I can see this behavior on the graph, if I zoom out on the x-axis:
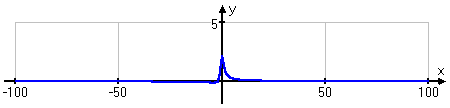
The graph shows that there's some slightly interesting behavior in the middle, right near the origin, but the rest of the graph is fairly boring, trailing along the x-axis.
If I zoom in on the origin, I can also see that the graph crosses the horizontal asymptote (at the arrow):
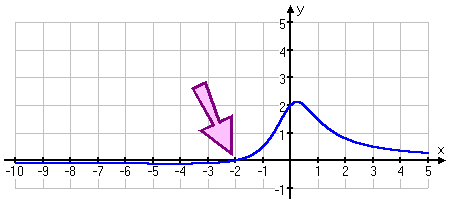
It is common and perfectly okay to cross a horizontal asymptote. (It's the vertical asymptotes that I'm not allowed to touch.)
As I can see in the table of values and from the graph, the horizontal asymptote is the x-axis.
horizontal asymptote: y = 0 (the x-axis)
In the above example, the degree on the denominator (namely, 2) was bigger than the degree on the numerator (namely, 1), and the horizontal asymptote was y = 0 (that is, it was the x-axis). This property is always true: If the degree on x in the denominator is larger than the degree on x in the numerator, then the denominator, being stronger, pulls the fraction down to the x-axis when x gets big.
That is, if the polynomial in the denominator has a bigger leading exponent than the polynomial in the numerator, then the graph trails along the x-axis at the far right and the far left of the graph. So any time the power on the denominator is larger than the power on the numerator, the horizontal asymptote is going to be the the x-axis, also known as the line y = 0.
What happens if the degrees are the same in the numerator and denominator? Let's take a look:
-
Find the horizontal asymptote of the following:
![y = [2x^2 − 11] / [x^2 + 9]](rational/asympt13.gif){kind=small}
Like the previous example, this denominator has no zeroes, so there are no vertical asymptotes.
Unlike the previous example, this function has degree-2 polynomials top and bottom; in particular, the degrees are the same in the numerator and the denominator. Since the degrees are the same, the numerator and denominator "pull" evenly; this graph should not drag down to the x-axis, nor should it shoot off to infinity. But where will it go?
Again, I need to think in terms of big values for x. When x is really big, I'll have, roughly, twice something big (minus an eleven, but who cares about that?) divided by once something big (plus a nine, but who cares about that?).
As you might guess from the last exercise, the –11 and the +9 won't matter much for really big values of x. Far off to the sides of the graph, I'll roughly have , which reduces to just 2.
Does a table of values bear this out? Let's check:
x |
![y = [2x^2 − 11] / [x^2 + 9]](rational/asympt14.gif){kind=small} |
−100 000 |
1.9999999... |
−10 000 |
1.9999997... |
−1 000 |
1.9999710... |
−100 |
1.9971026... |
−10 |
1.7339449... |
−1 |
–0.9 |
0 |
−1.2222222... |
1 |
−0.9 |
10 |
1.7339449... |
100 |
1.9971026... |
1 000 |
1.9999710... |
10 000 |
1.9999997... |
100 000 |
1.9999999... |
For big values of x, the value of the function is, as expected, very close to y = 2. And the graph of the function reflects this:
![graph of y = [2x^2 − 11] / [x^2 + 9]](rational/asympt15.gif)
Sure, there's probably something interesting going on in the middle of the graph, near the origin. But, off to the sides, the graph is clearly sticking very close to the line y = 2. (In calculus, you'll learn how to prove this yourself.)
Then my answer is:
horizontal asymptote: y = 2
In the example above, the degrees on the numerator and denominator were the same, and the horizontal asymptote turned out to be the horizontal line whose y-value was equal to the value found by dividing the leading coefficients of the two polynomials. This is always true: When the degrees of the numerator and the denominator are the same, then the horizontal asymptote is found by dividing the leading terms, so the asymptote is given by:
y = (numerator's leading coefficient) / (denominator's leading coefficient)
What does the horizontal asymptote tell you?
The horizontal asymptote tells you where your graph goes, off to the sides, as x gets very large (positively or negatively).
-
Find the horizontal asymptote of .
Now that I know the rules about the powers, I don't have to do a table of values or draw the graph. I can just compare exponents.
In this rational function, the highest power in each of the numerator and the denominator is the same; namely, the cube.
(This fraction might feel a little bit misleading, because the highest-power term in the denominator is not the first term. But that's okay; all I need to find is whichever term has the largest exponent. It doesn't matter where, within the expression, that term happens to be located.)
So I know that this function's graph will have a horizontal asymptote which is the value of the division of the coefficients of the terms with the highest powers. Those coefficients are 4 and −3. Then my answer is:
hor. asymp.:
-
Find the horizontal asymptote of
The highest power in the numerator is 2. There is an x2 in the denominator, but that doesn't matter, because the highest power in the denominator is 5.
Since the largest power underneath is bigger than the largest power on top, then the horizontal asymptote will be the horizontal axis.
hor. asymp.: y = 0
What are the three cases for horizontal asymptotes?
The three cases for horizontal asymptotes are these:
- The numerator has a smaller degree than the denominator.
- The numerator has the same degree as the denominator.
- The numerator has a larger (by 1) degree than the denominator.
(No, the third option above is not really a horizontal asymptote. However, some sources include this case in this topic, so I mentioned it. However, most sources, like textbooks, consider this case to be different in type.)
How do you find the horizontal asymptote?
To find the horizontal asymptote:
- When the numerator has a smaller degree, the horizontal asymptote is the x-axis (or, which is the same thing, the line y = 0)
- When the numerator has the same degree, the horizontal asymptote is found by dividing the coefficients of the terms with this degree; if the terms with this degree have coefficients n and d (for the numerator and denominator, respectively), then the horizontal asymptote is the line .
- When the numerator has a larger degree (by 1), the horizontal asymptote isn't actually horizontal, but is instead slanted (which we'll see on the next page).
© 2024 Purplemath, Inc. All right reserved. Web Design by 